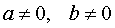Справочник по математике Элементы математического анализа
Элементы математического анализа Интегралы
Интегралы
Первообразная. Неопределенный интеграл. Правила интегрирования. Таблица интегралов. Примеры решения задач
Содержание
 |
Первообразная |
 |
Неопределенный интеграл |
 |
Правила интегрирования. Замена переменной в неопределенном интеграле |
 |
Таблица интегралов |
 |
Примеры решения задач |

Первообразная
ОПРЕДЕЛЕНИЕ 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого 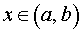 выполнено равенство
выполнено равенство
F' (x) = f (x) .
Например, из справедливости равенства
(sin 2x)' = 2 cos 2x
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
ЗАМЕЧАНИЕ. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
ТЕОРЕМА 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
F (x) + с ,
где c – некоторое число.
Неопределенный интеграл
ОПРЕДЕЛЕНИЕ 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
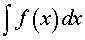 |
(1) |
Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
 |
(2) |
Однако для упрощения формулу (2) принято записывать в виде
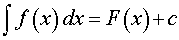 |
(3) |
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx называют подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
ПРАВИЛО 1 (интеграл от произведения числа на функцию). Справедливо равенство
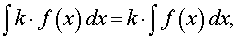
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
ПРАВИЛО 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле
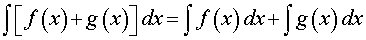
то есть интеграл от суммы функций равен сумме интегралов от этих функций.
ПРАВИЛО 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле
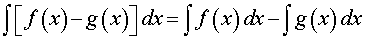
то есть интеграл от разности функций равен разности интегралов от этих функций.
ПРАВИЛО 4 (интегрирование при помощи замены переменной). Из справедливости формулы
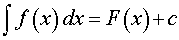
вытекает, что
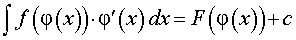 |
(4) |
если все входящие в формулу (4) функции f (φ (x)), φ' (x), F (φ (x)) определены.
ДОКАЗАТЕЛЬСТВО ПРАВИЛА 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):
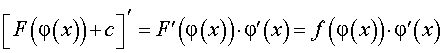
Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
ЗАМЕЧАНИЕ. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
φ (x) = kx + b ,
что k и b – произвольные числа, 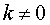 .
.
В этом случае
φ' (x) = k ,
и формула (4) принимает вид
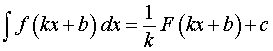 |
(5) |
Формула (5) часто используется при решении задач.
Таблица интегралов
Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций
|
Основная формула:
Обобщения: |
|
где n – любое число, не равное – 1 . Обобщения:
где n, k, b – любые числа, _____
где n – любое число, |
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
|
Основная формула:
где a – любое положительное число, не равное 1 . Обобщения:
где a – любое положительное число, не равное 1, k, b – любые числа, _____
|
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
|
Основная формула:
где Обобщения:
где k, b – любые числа, _____
где |
|
Основная формула:
где Обобщения:
где k, b – любые числа, _____
|
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
где | φ (x) | < 1 _____
|
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
_____
где a, b – любые числа, |
Примеры решения задач
ПРИМЕР 1. Вычислить интеграл
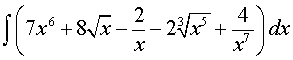
РЕШЕНИЕ. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов, получаем
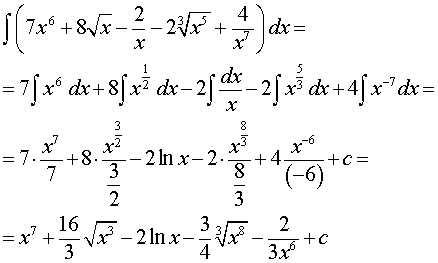
ОТВЕТ.
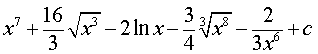
ПРИМЕР 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти 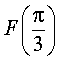 .
.
РЕШЕНИЕ. Поскольку
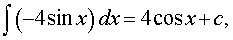
то
| F (x) = 4 cos x + c, | (6) |
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:
F (0) = 4 cos 0 + c = 9,
4 + c = 9, c = 5.
Следовательно,
F (x) = 4 cos x + 5
Поэтому
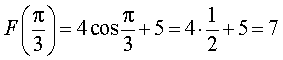
ОТВЕТ. 7
ПРИМЕР 3. Найти первообразную F (x) функции
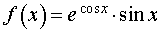
если F (2π) = 2e + 3.
РЕШЕНИЕ. Воспользовавшись формулой из таблицы неопределенных интегралов
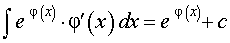
для функции φ (x) = cos x , получаем
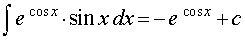
Следовательно,
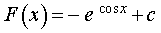 |
(7) |
Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:
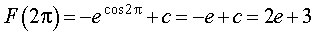
Итак,
c = 3e +3 .
ОТВЕТ. 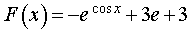
ПРИМЕР 4. Вычислить интеграл
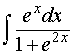
РЕШЕНИЕ. Воспользовавшись формулой из таблицы неопределенных интегралов
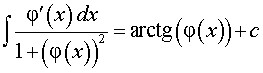
для функции φ (x) = ex, получаем
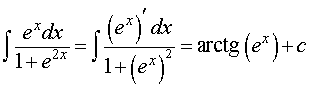
ОТВЕТ. 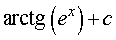
Близкие по тематике разделы сайта
С более подробным и расширенным изложением материала «Интегральное исчисление функций одной переменной» можно ознакомиться в учебно-методическом пособии: «Интегральное исчисление функций одной переменной».
Способы вычисления неопределенных интегралов можно посмотреть также в пособиях
- «Неопределенный интеграл. Простейшие приемы интегрирования»,
- «Интегрирование рациональных дробей»,
- «Интегрирование иррациональных функций»,
- «Интегрирование выражений, содержащих тригонометрические и гиперболические функции»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 2 семестр)».

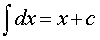
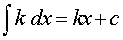 , где
, где 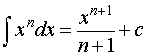
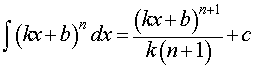 ,
,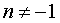
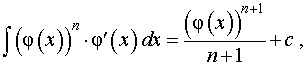
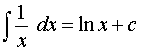 ,
,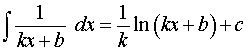 ,
,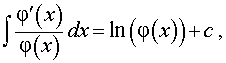
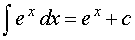
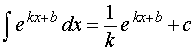 ,
,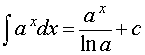 ,
,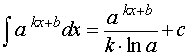 ,
,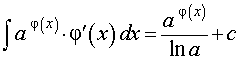 ,
,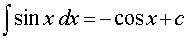
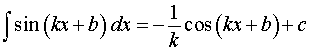 ,
,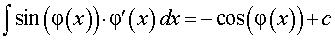
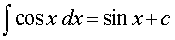
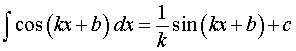 ,
,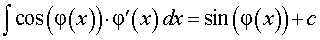
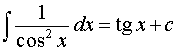
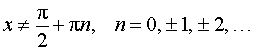
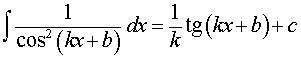 ,
,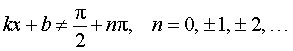
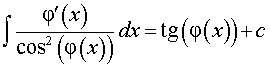 ,
,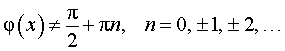
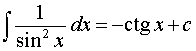
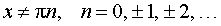
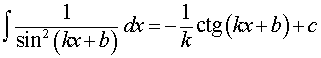 ,
,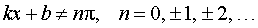
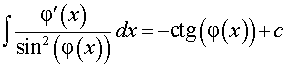 ,
,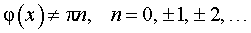
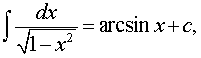
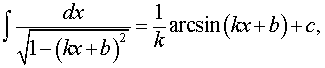
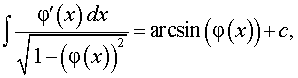
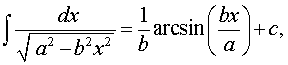
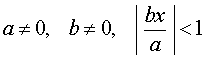
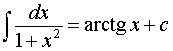
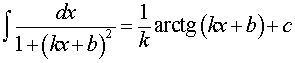 ,
,