Справочник по математике Элементы математического анализа
Элементы математического анализа Производная функции
Производная функции
Исследование поведения функций с помощью производной
Содержание

Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,
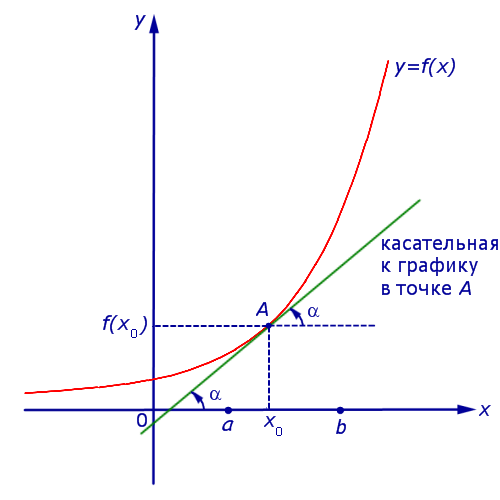
Рис.1
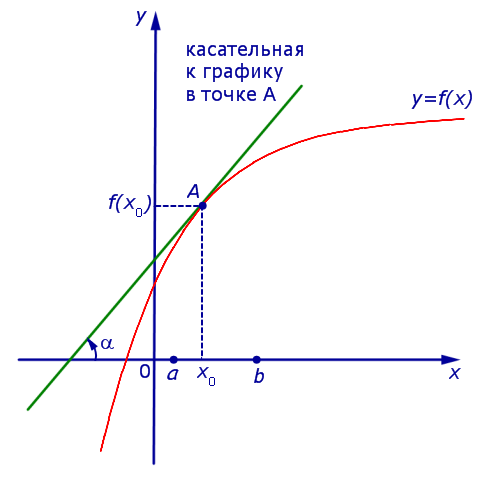
Рис.2
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
f ' (x0) = tg α > 0
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
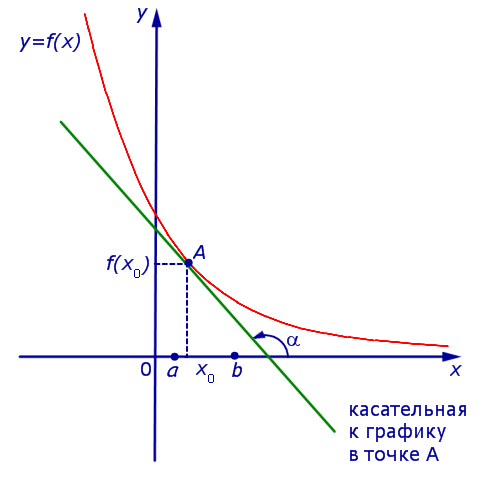
Рис.3
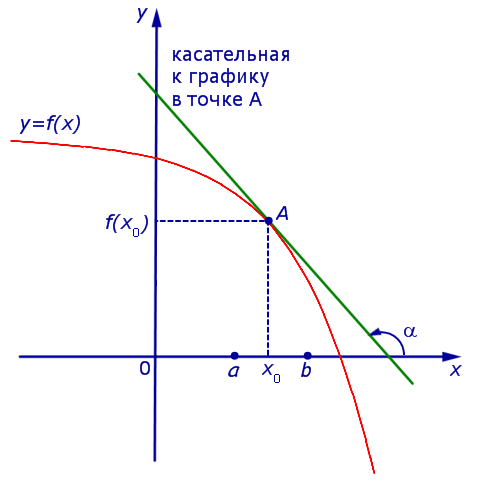
Рис.4
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
f ' (x0) = tg α < 0
Достаточные условия для возрастания и убывания функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики, сформулированы достаточные условия для возрастания и убывания функции.
УТВЕРЖДЕНИЕ 1.
а). Если в каждой точке x интервала (a, b) производная f ' (x) существует и удовлетворяет неравенству
f ' (x) > 0 ,
то функция f (x) строго возрастает на интервале (a, b) .
б). Если в каждой точке x интервала (a, b) производная f ' (x) существует и удовлетворяет неравенству
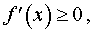
то функция f (x) возрастает (не убывает) на интервале (a, b) .
в). Если в каждой точке x интервала (a, b) производная f ' (x) существует и удовлетворяет неравенству
f ' (x) < 0 ,
то функция f (x) строго убывает на интервале (a, b) .
г). Если в каждой точке x интервала (a, b) производная f ' (x) существует и удовлетворяет неравенству
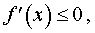
то функция f (x) убывает (не возрастает) на интервале (a, b) .
Экстремумы (максимумы и минимумы) функции
ОПРЕДЕЛЕНИЕ 1. Точку x0 называют точкой максимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
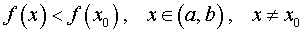 .
.
Таким образом, если x0 – точка максимума функции f (x) , то в интервале (a, b) значение функции f (x0) больше всех остальных значений функции.
ОПРЕДЕЛЕНИЕ 2. Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
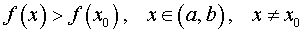 .
.
Другими словами, если x0 – точка минимума функции f (x) , то в интервале (a, b) значение функции f (x0) меньше всех остальных значений функции.
ОПРЕДЕЛЕНИЕ 3. Точки максимума и минимума функции называют точками экстремума функции, а значения функции в точках экстремума называют экстремумами функции.
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
ОПРЕДЕЛЕНИЕ 4. Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.
ОПЕРЕДЕЛЕНИЕ 5. Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
ТЕОРЕМА ФЕРМА. Если точка x0 является точкой экстремума функции f (x) , то точка x0 является критической точкой функции f (x) .
ДОКАЗАТЕЛЬСТВО. Если в точке x0 у функции y = f (x) не существует производная, то точка x0 является критической точкой по определению. Докажем, что если в точке x0 у функции y = f (x) существует производная, то точка x0 является стационарной, то есть f ' (x0) = 0 .
Предположим сначала, что точка x0 является точкой максимума функции y = f (x) (рис. 5).
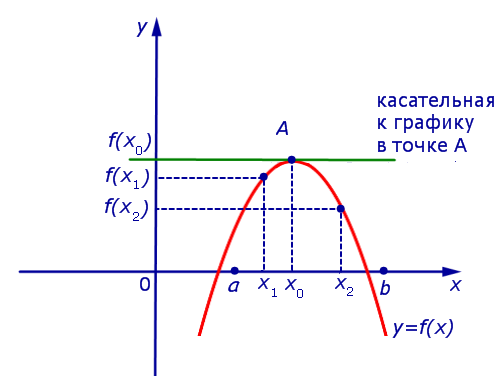
Рис.5
Поскольку x0 – точка максимума, то для любой точки x1 такой, что x1< x0 , выполнено неравенство f (x1) < f (x0) , поэтому
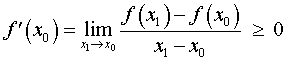 .
.
Точно так же, для любой точки x2 такой, что x2 > x0 , выполнено неравенство f (x2) < f (x0) , поэтому
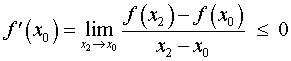 .
.
Таким образом, в случае, когда точка x0 является точкой максимума функции y = f (x), выполнено равенство f ' (x0) = 0 . Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox.
Совершенно аналогично доказывается, что и в случае, когда точка x0 является точкой минимума функции y = f (x), выполнено равенство f ' (x0) = 0 .
ЗАМЕЧАНИЕ 1. Из утверждения 2 следует, что точки экстремумов функции (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум.
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
УТВЕРЖДЕНИЕ 3. Рассмотрим функцию f (x) , непрерывную в интервале (a, b), содержащем точку x0 , производная которой существует в каждой точке этого интервала, кроме, быть может, самой точки x0 .
а). Если для точек 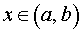 выполнено условие:
выполнено условие:
f ' (x) > 0 при x < x0 и f ' (x) < 0 при x > x0 ,
то точка x0 является точкой максимума функции f (x) (рис. 6).
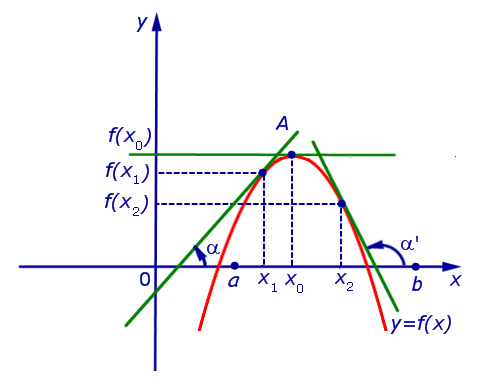
Рис.6
б). Если для точек 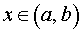 выполнено условие:
выполнено условие:
f ' (x) < 0 при x < x0 и f ' (x) > 0 при x > x0 ,
то точка x0 является точкой минимума функции f (x) (рис. 7).
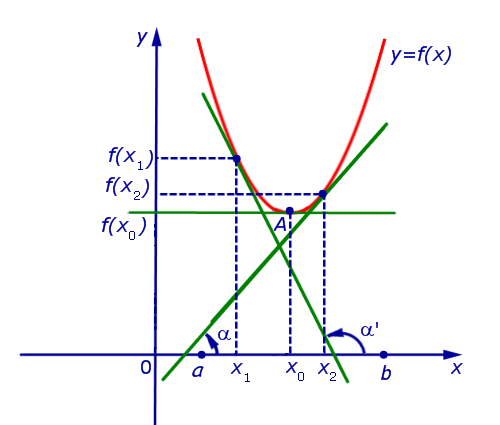
Рис.7
ЗАМЕЧАНИЕ 2. Условия а) и б) утверждения 3 часто формулируют так: «Если при переходе через точку x0 производная функции меняет знак с «+» на «–» , то точка x0 является точкой максимума функции. Если при переходе через точку x0 производная функции меняет знак с «–» на «+» , то точка x0 является точкой минимума функции».
Пример исследования поведения функции
ПРИМЕР. Найти интервалы возрастания, убывания и экстремумы функции
| y = | x3 + 3x2 | | (1) |
РЕШЕНИЕ. Исследуем сначала на возрастание, убывание и экстремумы функцию
| y1 = x3 + 3x2 | (2) |
и построим ее график. Для этого представим формулу (2) в виде
y1 = x2 (x + 3)
и заметим, что
а) y1 = 0 при x = 0 и x = – 3 ,
б) y1 > 0 при x > – 3 ; y1 < 0 при x < – 3 .
Теперь вычислим производную функции (2):
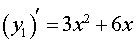 |
(3) |
и разложим на множители правую часть формулы (3):
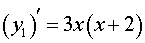 |
(4) |
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
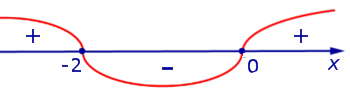
Рис.8
Поскольку решением неравенства
3x (x + 2) > 0
является множество
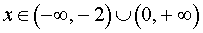 , , |
(5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов 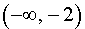 и
и 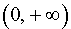 .
.
С другой стороны, поскольку решением неравенства
3x (x + 2) < 0
является интервал
| (– 2, 0), | (6) |
то в соответствии с утверждением 1 функция y1 убывает на интервале (– 2, 0) .
Так как решениями уравнения
3x (x + 2) = 0
являются точки
| x = – 2; x = 0; | (7) |
то эти точки являются стационарными точками функции y1 .
Поскольку при переходе через точку x = – 2 производная функции y1 меняет знак с «+» на «–» (рис. 8), то в соответствии с утверждением 3 точка x = – 2 является точкой максимума функции y1 , при этом
y1 (– 2) = 4 .
При переходе через точку x = 0 производная функции y1 меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с утверждением 3 точка x = 0 является точкой минимума функции y1, при этом
y1 (0) = 0 .
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
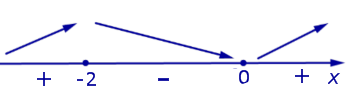
Рис.9
Теперь мы можем построить график функции y1 (рис. 10).
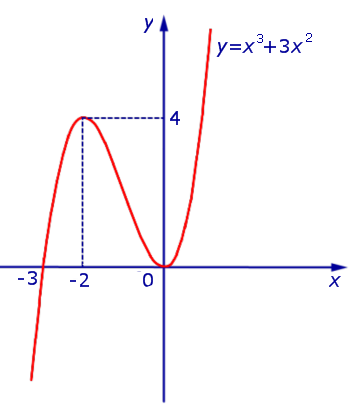
Рис.10
Перейдем к построению графика функции y = | x3 + 3x2 | .
В силу определения модуля, справедливо равенство
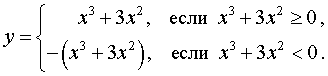
Из этого равенства вытекает, что, если мы симметрично отразим относительно оси Ox часть графика функции y1 = x3 + 3x2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3x2 | (рис.11) .
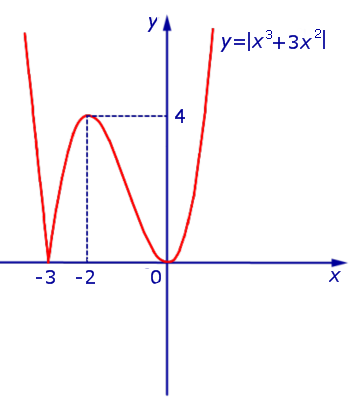
Рис.11
В точке x = – 3 производная функции y = | x3 + 3x2 | не существует. Во всех остальных точках числовой оси производная функции y = | x3 + 3x2 | существует.
Точки x = – 3 и x = 0 являются точками минимума, причем y ( – 3) = y (0) = 0 .
Точка x = – 2 является точкой максимума, причем y ( – 2) = 4 .
Функция y = | x3 + 3x2 | возрастает на каждом из интервалов (– 3, – 2) и 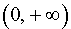 .
.
Функция y = | x3 + 3x2 | убывает на каждом из интервалов 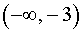 и (– 2, 0).
и (– 2, 0).
Близкие по тематике разделы сайта
С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»
Исследование функций с помощью производных и примеры построения графиков функций можно посмотреть в учебных пособиях:
- «Исследование функций с помощью производных. Построение графиков (часть 1)»
- «Исследование функций с помощью производных. Построение графиков (часть 2)»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».

