Справочник по математикеЭлементы математического анализа Производная функции

Приращение аргумента и приращение функции. Производная как предел отношения приращений. Непрерывность функции

Содержание

	Приращение аргумента и приращение функции. Производная как предел отношения приращений
	Непрерывность функции

Приращение аргумента и приращение функции. Производная как предел отношения приращений

В разделе «Секущая графика функции. Касательная к графику функции. Производная функции. Геометрический смысл производной» нашего справочника приведено определение производной функции   y = f (x)   в точке   x₀   (в том случае, если она существует) как числа, к которому стремится отношение

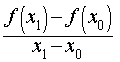(1)

при   x₁ → x₀ .   Коротко это принято записывать так:

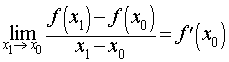(2)

Заметим, что существование производной функции   y = f (x)   и значение производной зависят от выбора точки   x₀ . Поэтому производная функции сама является функцией точки   x₀ .

Если в формуле (2) заменить  x₀   на   x ,   а разность  x₁ – x₀   обозначить символом  Δx,   то эта формула примет вид

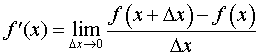(3)

ОПРЕДЕЛЕНИЕ 1. Переменную   Δx   называют приращением аргумента,  а разность

f (x + Δx) – f (x)

называют приращением функции   f (x) в точке   x ,   соответствующим приращению аргумента   Δx,   и обозначают  Δf .

Таким образом,

Используя определения приращения аргумента и приращения функции, формулу (3) можно переписать так:

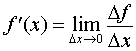(5)

В соответствии с этой формулой производную функции    f (x)   в точке   x   называют пределом отношения приращения функции к приращению аргумента в точке   x ,   когда приращение аргумента стремится к нулю.

ПРИМЕР 1. Вывести формулу для производной функции   y = x² .

РЕШЕНИЕ. Из формулы (3) получаем:

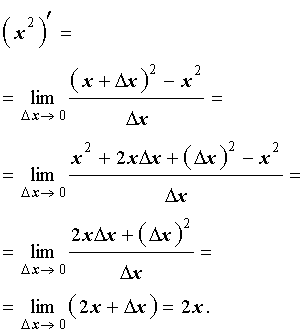
ОТВЕТ.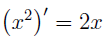

Непрерывность функции

ОПРЕДЕЛЕНИЕ 2. Функцию   y = f (x)   называют непрерывной в точке   x₀ ,   если выполнено равенство

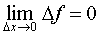(6)

Другими словами, функция   f (x)   непрерывна в точке   x₀   тогда и только тогда, когда выполнено равенство

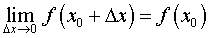(7)

ПРИМЕР 2. Доказать, что функция   y = x³   непрерывна в любой точке   x ,   где .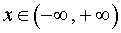

РЕШЕНИЕ. Выберем произвольную точку   x,   где 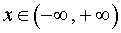, и воспользуемся формулой сокращенного умножения «куб суммы»:

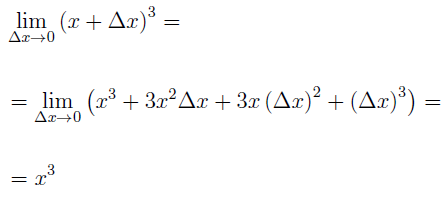
Соотношение (7) выполнено, что и завершает решение примера 2.

ПРИМЕР 3. Доказать, что функция

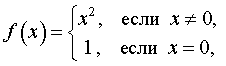(8)

разрывна (не является непрерывной) в точке   x = 0 .

РЕШЕНИЕ. Поскольку в точке   x = 0

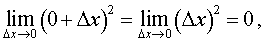
причем

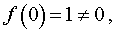
то соотношение (7) в точке   x = 0   не выполняется. Таким образом, функция (8) является разрывной в точке   x = 0 .

Доказано.

Для наглядности приведем график функции (8) (рис. 1).

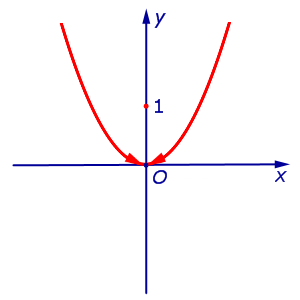
Рис.1

ЗАМЕЧАНИЕ. Если в точке   x = x₀   у функции    f (x)   существует производная, то функция    f (x)   непрерывна в точке  x₀ .

Обратное утверждение, вообще говоря, неверно: если функция    f (x)   непрерывна в точке   x₀ ,   то отсюда вовсе не следует, что в этой точке у функции должна существовать производная. Примером является функция    f (x) = |x|   (модуль   x), которая непрерывна в точке   x = 0 ,   но у нее не существует производной в этой точке.

Близкие по тематике разделы сайта

С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»

Исследование функций с помощью производных и примеры построения графиков функций можно посмотреть в учебных пособиях:

• «Исследование функций с помощью производных. Построение графиков (часть 1)»
• «Исследование функций с помощью производных. Построение графиков (часть 2)»

на странице  «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».