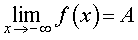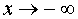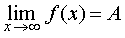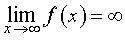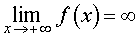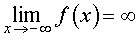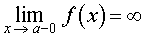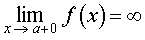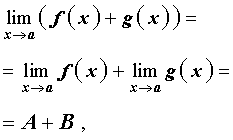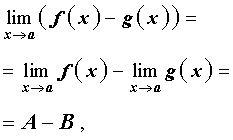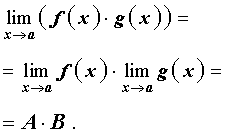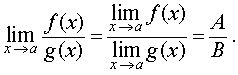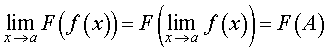Справочник по математике Элементы математического анализа
Элементы математического анализа Функции
Функции
Пределы функций
Содержание
 |
Предел функции |
 |
Свойства пределов функций |
 |
Раскрытие неопределенностей типа 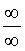 |
 |
Раскрытие неопределенностей типа 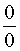 |
 |
Первый замечательный предел |
 |
Раскрытие неопределенностей типа 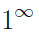 . Второй замечательный предел . Второй замечательный предел |

Предел функции
В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.
Свойства пределов функций
Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы
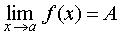 и
и 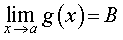 ,
,
где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем
|
|
|
|
|
|
Если, кроме того, выполнено условие
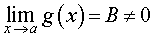
то при x , стремящемся к a , существует предел дроби
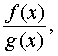
причем
|
|
Для любой непрерывной функции F (x) справедливо равенство
|
|
Раскрытие неопределенностей типа 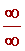
ОПРЕДЕЛЕНИЕ 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к , то вычисление такого предела называют раскрытием неопределенности типа
, то вычисление такого предела называют раскрытием неопределенности типа 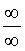 .
.
Часто неопределенность типа 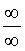 удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
ПРИМЕР 1. Найти предел функции
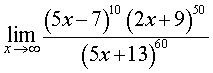
РЕШЕНИЕ. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства степеней и свойства пределов функций, получим
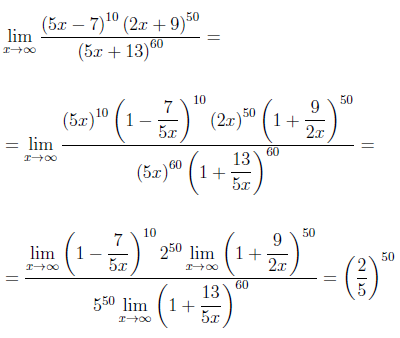
ОТВЕТ. 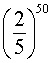
ПРИМЕР 2. Найти предел функции
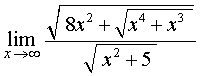
РЕШЕНИЕ. С помощью свойств корней преобразуем выражение, стоящее под знаком предела, к более удобному виду:
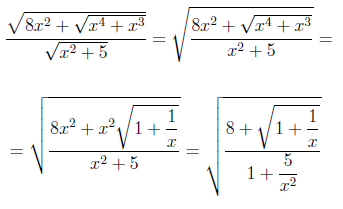
Далее, используя свойства пределов функций, находим
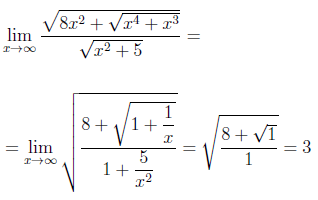
ОТВЕТ. 3 .
Раскрытие неопределенностей типа 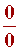
ОПРЕДЕЛЕНИЕ 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности 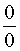 .
.
В алгебраических дробях неопределенность 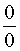 при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .
при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .
ПРИМЕР 3. Найти предел функции
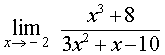
РЕШЕНИЕ. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа 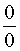 , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :
, разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :
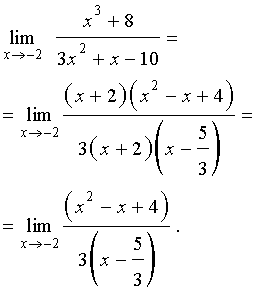
Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем
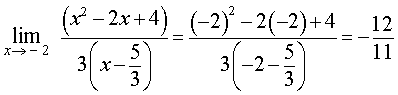
ОТВЕТ. 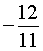
ПРИМЕР 4. Найти предел функции
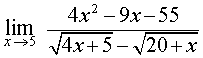
РЕШЕНИЕ. В этом примере также возникает неопределенность типа 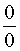 .
.
Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то домножим и числитель, и знаменатель дроби на сумму этих квадратных корней и применим формулу сокращенного умножения «разность квадратов»:
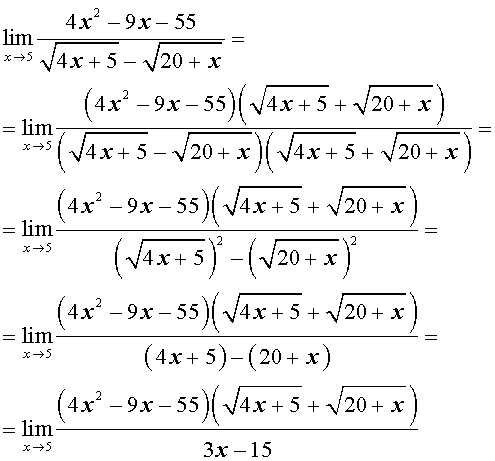
Разложим теперь квадратный трехчлен 4x2 – 9x – 55 на множители, а затем сократим числитель и знаменатель на (x – 5) :
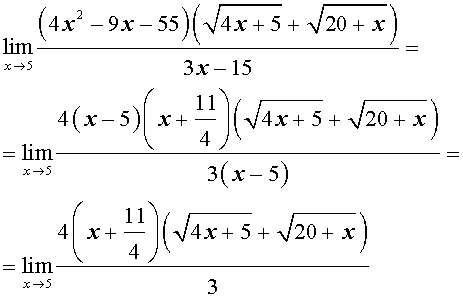
Воспользовавшись свойствами пределов функций, получаем
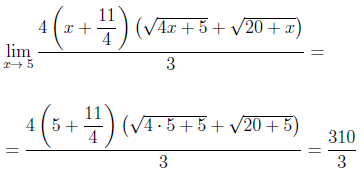
ОТВЕТ. 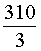
Первый замечательный предел
В пределах, содержащих тригонометрические функции, неопределенность 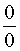 раскрывается с помощью первого замечательного предела
раскрывается с помощью первого замечательного предела
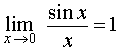
ПРИМЕР 5. Найти предел функции
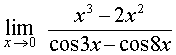
РЕШЕНИЕ. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа 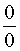 , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x2, а в знаменателе воспользуемся формулой «разность косинусов»:
, разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x2, а в знаменателе воспользуемся формулой «разность косинусов»:
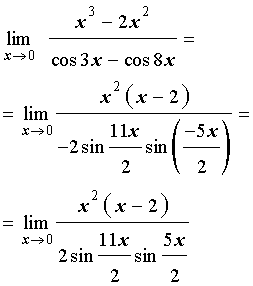
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
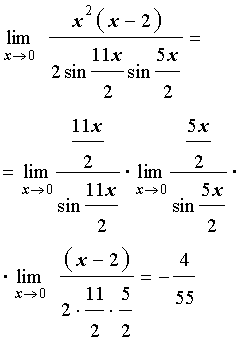
ОТВЕТ. 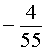
ПРИМЕР 6. Найти предел функции
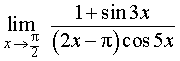
РЕШЕНИЕ. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле
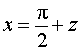 .
.
Поскольку
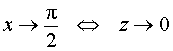 ,
,
то предел можно преобразовать к виду
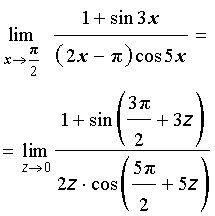
Применяя формулы приведения и формулу для косинуса двойного угла, получаем
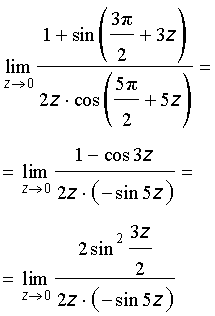
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
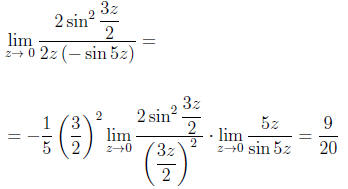
ОТВЕТ. 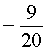
Раскрытие неопределенности типа 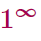 . Второй замечательный предел
. Второй замечательный предел
ОПРЕДЕЛЕНИЕ 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен  , то вычисление такого предела называют раскрытием неопределенности
, то вычисление такого предела называют раскрытием неопределенности 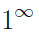 .
.
Неопределенность 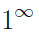 раскрывается с помощью второго замечательного предела:
раскрывается с помощью второго замечательного предела:
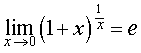 . . |
(1) |
Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:
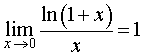 |
(2) |
ПРИМЕР 7. Найти предел функции
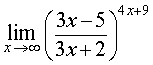
РЕШЕНИЕ. Рассмотрим функцию
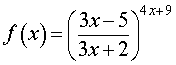
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → . Применяя свойства логарифмов, получаем
. Применяя свойства логарифмов, получаем
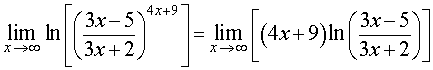
Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,
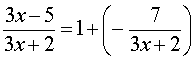
и заметим, что
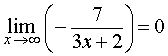
Поэтому, воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, находим
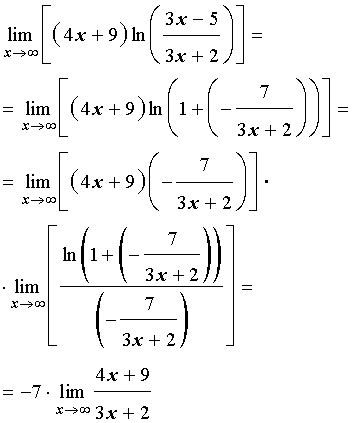
В пределе
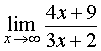
и числитель, и знаменатель дроби стремятся к , поэтому для раскрытия неопределенности
, поэтому для раскрытия неопределенности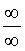 вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим
вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим
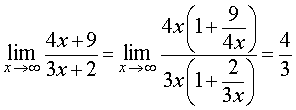
Следовательно,
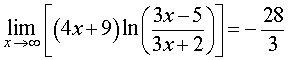
Таким образом,
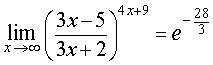
ОТВЕТ. 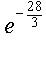
ПРИМЕР 8. Найти предел функции
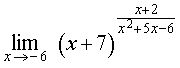
РЕШЕНИЕ. Рассмотрим функцию
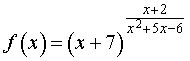
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем
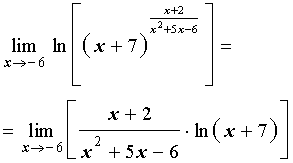 |
(3) |
Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле
x = – 6 + z .
Поскольку
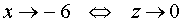
то предел (3) можно преобразовать к виду
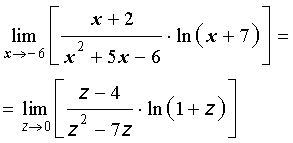
Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем
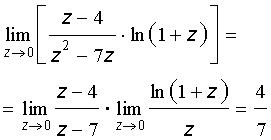
Следовательно,
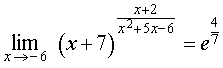
ОТВЕТ. 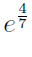
Близкие по тематике разделы сайта
С материалами, связанными со свойствами функций и их пределами, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»

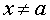 , удовлетворяющих неравенству
, удовлетворяющих неравенству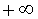 , равен числу
, равен числу 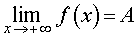
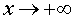
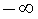 , равен числу
, равен числу