Справочник по математике Элементы математического анализа
Элементы математического анализа Числовые последовательности
Числовые последовательности
Числовые последовательности
Содержание
 |
Числовые последовательности. Способы задания числовых последовательностей |
 |
Возрастающие и убывающие последовательности |
 |
Ограниченные и неограниченные последовательности |

Числовые последовательности. Способы задания числовых последовательностей
Если каждому натуральному числу n поставлено в соответствие некоторое действительное число xn , то говорят, что задана числовая последовательность
x1 , x2 , … xn , …
Число x1 называют членом последовательности с номером 1 или первым членом последовательности, число x2 - членом последовательности с номером 2 или вторым членом последовательности, и т.д. Число xn называют членом последовательности с номером n .
Существуют два способа задания числовых последовательностей – с помощью формулы общего члена последовательности и с помощью рекуррентной формулы.
Задание последовательности с помощью формулы общего члена последовательности – это задание последовательности
x1 , x2 , … xn , …
с помощью формулы, выражающей зависимость члена xn от его номера n .
ПРИМЕР 1. Числовая последовательность
1, 4, 9, … n2 , …
задана с помощью формулы общего члена
xn = n2, n = 1, 2, 3, …
Задание последовательности с помощью формулы, выражающей член последовательности xn через члены последовательности с предшествующими номерами, называют заданием последовательности с помощью рекуррентной формулы.
ПРИМЕР 2 (Числа Фибоначчи). Числовая последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
может быть задана с помощью рекуррентной формулы
xn = xn – 1 + xn – 2 , n > 2 ,
с начальными условиями
x1 = 1, x2 = 1 .
Возрастающие и убывающие последовательности
ОПРЕДЕЛЕНИЕ 1. Числовую последовательность
x1 , x2 , … xn , …
называют возрастающей последовательностью, если каждый член этой последовательности больше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn + 1 > xn
ПРИМЕР 3. Последовательность натуральных чисел
1, 2, 3, … n, …
является возрастающей последовательностью.
ОПРЕДЕЛЕНИЕ 2. Числовую последовательность
x1 , x2 , … xn , …
называют убывающей последовательностью, если каждый член этой последовательности меньше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn + 1 < xn
ПРИМЕР 4. Последовательность
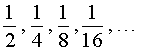
заданная формулой
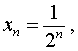
является убывающей последовательностью.
ПРИМЕР 5. Числовая последовательность
1, – 1, 1, – 1, …
заданная формулой
xn = (– 1)n, n = 1, 2, 3, …
не является ни возрастающей, ни убывающей последовательностью.
ОПРЕДЕЛЕНИЕ 3. Возрастающие и убывающие числовые последовательности называют монотонными последовательностями.
Ограниченные и неограниченные последовательности
ОПРЕДЕЛЕНИЕ 4. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn < M
ОПРЕДЕЛЕНИЕ 5. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn > m
ОПРЕДЕЛЕНИЕ 6. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной, если она ограничена и сверху, и снизу.
Другими словами, существуют такие числа M и m, что для всех n = 1, 2, 3, … выполнено неравенство
m < xn < M
ОПРЕДЕЛЕНИЕ 7. Числовые последовательности, которые не являются ограниченными, называют неограниченными последовательностями.
ПРИМЕР 6. Числовая последовательность
1, 4, 9, … n2 , …
заданная формулой
xn = n2, n = 1, 2, 3, … ,
ограничена снизу, например, числом 0. Однако эта последовательность неограничена сверху.
ПРИМЕР 7 . Последовательность
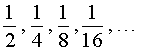
заданная формулой
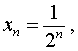
является ограниченной последовательностью, поскольку для всех n = 1, 2, 3, … выполнено неравенство
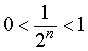
Близкие по тематике разделы сайта
С последовательностями и их пределами можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»
