Справочник по математикеЭлементы математического анализа Производная функции

Примеры вычисления производных

ПРИМЕР 1. Найти производную функции

y = cos 2x

РЕШЕНИЕ. Воcпользовавшись формулой для производной сложной функции   y = cos (kx + b)   в случае, когда   k = 2,   b = 0,   получим

(cos 2x)' = – 2sin 2x .

ЗАМЕЧАНИЕ. Очень часто школьники, а также и студенты, при решении примера 1 пишут:

(cos 2x)' = – sin 2x .

Это ошибка !!!

Перепишем верный ответ еще раз:

(cos 2x)' = – 2sin 2x .

Приведем также верные ответы в похожих примерах:

(sin 3x)' = 3cos 3x ,

,

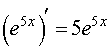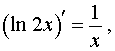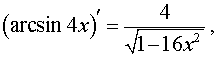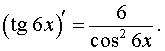ПРИМЕР 2. Найти производную функции

y = sin³x

РЕШЕНИЕ. Воcпользовавшись формулой для производной сложной функции   y = ( f (x)) ^c   в случае, когда   f (x) = sin x ,   а   c = 3,   получим

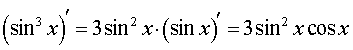
ОТВЕТ: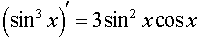

ПРИМЕР 3. Найти производную функции

y = (3x – 7)⁵ .

РЕШЕНИЕ. Воcпользовавшись формулой для производной сложной функции   y = (kx + b)^c   в случае, когда   k = 3,   b = – 7,   а   c = 5,   получим

y' = 15(3x – 7)⁴ .

ОТВЕТ: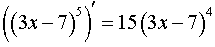

ПРИМЕР 4. Найти производную функции

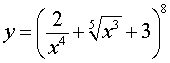
РЕШЕНИЕ. Поскольку

,

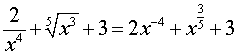то исходную функцию можно переписать в виде

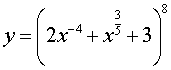
Воcпользовавшись формулой для производной сложной функции   y = ( f (x)) ^c   в случае, когда

,

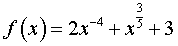а   c = 8,   получим

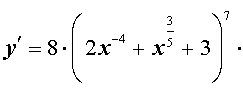
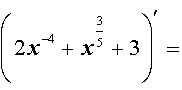
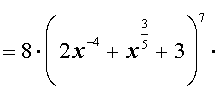
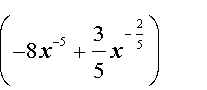
ОТВЕТ:

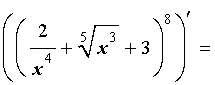
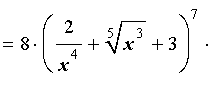
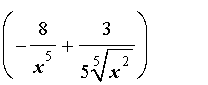
ПРИМЕР 5 . Найти производную функции

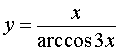
РЕШЕНИЕ. Воcпользовавшись правилом 5 для вычисления производной частного двух функций и формулой для производной сложной функции   y = arccos (kx + b)   в случае, когда   k = 3,   b = 0,   получим

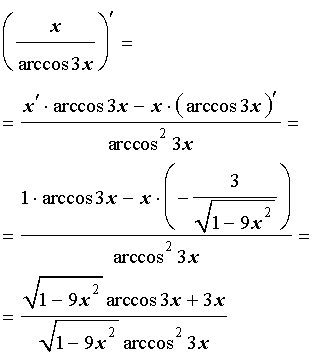
ОТВЕТ:

.

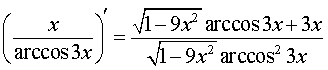ПРИМЕР 6. Найти производную функции

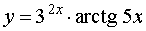
РЕШЕНИЕ. Воcпользовавшись правилом 4 для вычисления производной произведения двух функций, формулой для производной сложной функции   y = arctg (kx + b)   в случае, когда   k = 5,   b = 0, и формулой для производной сложной функции   y = a^kx + b   в случае, когда   a = 3,   k = 2,   b = 0,   получим

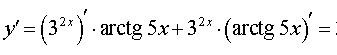
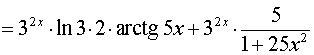
ОТВЕТ:

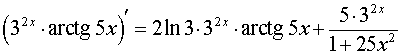
ПРИМЕР 7 . Найти производную функции

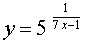
РЕШЕНИЕ. Поскольку

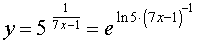
то, воcпользовавшись формулой для производной сложной функции   y = e ^f (x)   в случае, когда 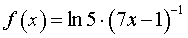  , и формулой для производной сложной функции   y = (kx + b)^c   в случае, когда   с = – 1,   k = 7,   b = – 1,  получим

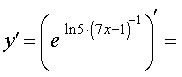
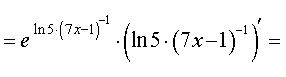
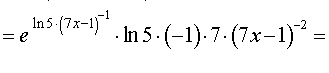
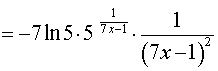
ОТВЕТ:

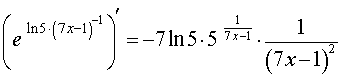
Близкие по тематике разделы сайта

С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»

Исследование функций с помощью производных и примеры построения графиков функций можно посмотреть в учебных пособиях:

• «Исследование функций с помощью производных. Построение графиков (часть 1)»
• «Исследование функций с помощью производных. Построение графиков (часть 2)»

на странице  «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».