Справочник по математикеЭлементы математического анализа Функции

Понятие функции. Область определения функции. Множество значений функции

Содержание

	Понятие функции. Область определения функции. Множество значений функции
	Примеры решения задач

Понятие функции. Область определения функции. Множество значений функции

ОПРЕДЕЛЕНИЕ. Пусть   X   – некоторое множество чисел. Говорят, что на множестве   X   задана числовая функция,  если указано правило, с помощью которого каждому числу   x   из множества   X   ставится в соответствие некоторое число.

Это принято обозначать так:

y = f (x),

причем в этой записи   x   называют аргументом функции  или независимой переменной, а   y   называют значением функции,  соответствующим аргументу   x .

Множество   X   называют областью определения функции   f   и обозначают   D ( f ) .   Множество   Y   всех возможных значений функции   y = f (x)   называют множеством значений функции   f   и обозначают   E ( f )  (рис. 1).

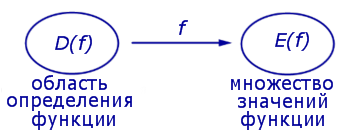
Рис.1

Примеры решения задач

Часто в задачах известна формула, задающая функцию   f ,   и требуется найти наиболее широкое множество чисел, к которым данную формулу можно применить. В этом случае указанная задача формулируется так: «Найти область определения функции   y = f (x)». В некоторых задачах требуется найти не только область определения функции, но и множество ее значений.

ЗАДАЧА 1. Найти область определения функции

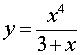
РЕШЕНИЕ. Указанная функцию представляет собой результат, полученный при делении числа   x⁴   на число   (3 + x) .   Поскольку единственным ограничением является запрет деления на число   0 ,   то число   (3 + x)   не может равняться   0 ,   то есть   .

ОТВЕТ.   .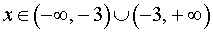

ЗАДАЧА 2. Найти область определения функции

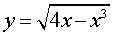
РЕШЕНИЕ. Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством

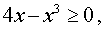
которое эквивалентно неравенству

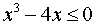
и может быть записано в виде

.

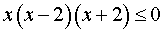Решая это неравенство с помощью метода интервалов, получим

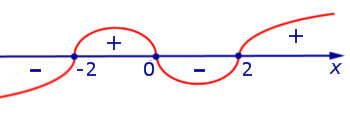
ОТВЕТ.   .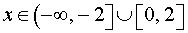

ЗАДАЧА 3. Найти область определения функции

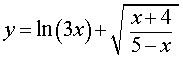
РЕШЕНИЕ. Исходя из определений логарифма и квадратного корня, область определения данной функции задается следующей системой неравенств

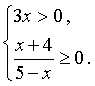(1)

Решая второе неравенство системы с помощью метода интервалов,

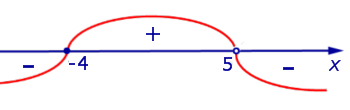
получим

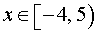
Таким образом, система (1) эквивалентна системе

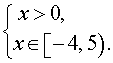
Решением этой системы является интервал

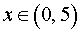
ОТВЕТ. .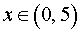

ЗАДАЧА 4 . Найти множество значений функции

y = 3sin x + 4cos x

РЕШЕНИЕ. Воспользовавшись формулой дополнительного угла (вспомогательного аргумента), получим

y = 5 sin (x + φ) ,

где

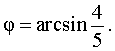
Поскольку множеством значений функции   y = sin (x + φ)   является отрезок   [–1, 1],   то множеством значений функции   y = 5 sin (x +φ)   будет отрезок   [–5, 5].

ОТВЕТ. .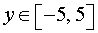

ЗАДАЧА 5 . Найти множество значений функции

y = x² + 6x + 8

РЕШЕНИЕ. Поскольку

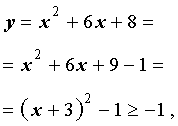
и для каждого числа 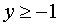существуют решения уравнения

x² + 6x + 8 = y ,

определяемые формулой

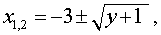
то множеством значений функции   y = x² + 6x + 8   будет множество   .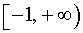

ОТВЕТ. .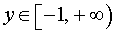

Близкие по тематике разделы сайта

С материалами, связанными со свойствами функций и их пределами, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»