Справочник по математикеЭлементы математического анализа Функции

Асимптоты графиков функций

Содержание

	Вертикальные асимптоты
	Наклонные асимптоты
	Горизонтальные асимптоты как частный случай наклонных асимптот
	Поиск наклонных асимптот графиков функций

Вертикальные асимптоты

Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.

ОПРЕДЕЛЕНИЕ 1. Говорят, что   x   стремится к   x₀   слева и обозначают

x → x₀ – 0 ,

если   x   стремится к   x₀   и   x   меньше   x₀ .  

Говорят, что   x   стремится к   x₀   справа и обозначают

x → x₀ + 0 ,

если   x   стремится к   x₀   и   x   больше   x₀ .

ОПРЕДЕЛЕНИЕ 2. Прямую

x = c

называют вертикальной асимптотой графика функции   y = f (x)   при   x ,   стремящемся к   с   справа, если функция   y = f (x)   определена на некотором интервале   (с, d)   и выполнено соотношение

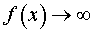при   x → c + 0

Прямую

x = с

называют вертикальной асимптотой графика функции   y = f (x)   при   x ,   стремящемся к   с   слева, если функция   y = f (x)   определена на некотором интервале   (d, c)   и выполнено соотношение

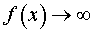при   x → c – 0

ПРИМЕР 1. Прямая

x = 2

является вертикальной асимптотой графика функции

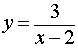
как справа, так и слева (рис. 1)

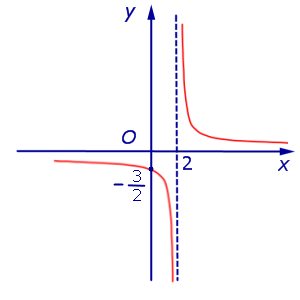
Рис.1

ПРИМЕР 2. Прямая

x = 0

является вертикальной асимптотой графика функции

y = ln x

при   x ,   стремящемся к   0   справа (рис. 2)

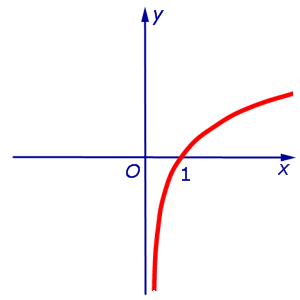
Рис.2

Наклонные асимптоты

ОПРЕДЕЛЕНИЕ 3. Прямую

y = kx + b

называют наклонной асимптотой графика функции   y = f (x)   при   x ,   стремящемся к 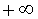, если функция   y = f (x)   определена на некотором интервале 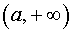и существует предел

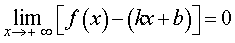
Прямую

y = kx + b

называют наклонной асимптотой графика функции   y = f (x)   при   x ,   стремящемся к 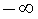, если функция   y = f (x)   определена на некотором интервале 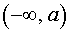и существует предел

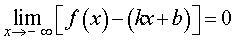
Горизонтальные асимптоты как частный случай наклонных асимптот

ОПРЕДЕЛЕНИЕ 4. Прямую

y = b

называют горизонтальной асимптотой графика функции   y = f (x)   при   x ,   стремящемся к 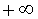, если функция   y = f (x)   определена на некотором интервале 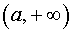и существует предел

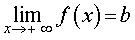
Прямую

y = b

называют горизонтальной асимптотой графика функции   y  f (x)   при   x ,   стремящемся к 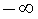, если функция   y = f (x)   определена на некотором интервале 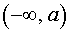и существует предел

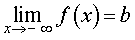
ЗАМЕЧАНИЕ. Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты   y = kx + b,   когда угловой коэффициент прямой   k = 0 .

ПРИМЕР 3. Прямая

y = 3

является горизонтальной асимптотой графика функции

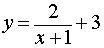
как при   x ,   стремящемся к 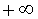, так и при   x ,   стремящемся к 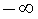(рис. 3)

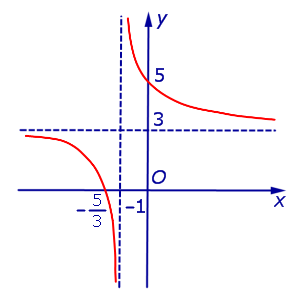
Рис.3

ПРИМЕР 4. Прямая

y = 0

является горизонтальной асимптотой графика функции

y = 2^x

при   x ,   стремящемся к 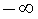(рис. 4)

Рис.4

ПРИМЕР 5. График функции  y = arctg x   (рис.5)

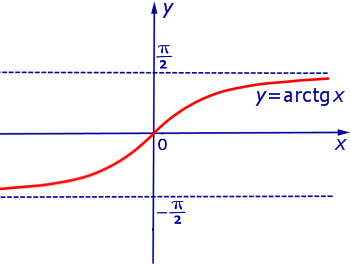
Рис.5

имеет две горизонтальные асимптоты: прямая

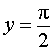
является горизонтальной асимптотой графика функции при 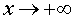, а прямая

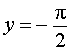
является горизонтальной асимптотой графика функции при .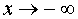

Поиск наклонных асимптот графиков функций

Для того, чтобы найти наклонную асимптоту графика функции   y = f (x)   при 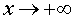(или убедиться, что наклонной асимптоты при 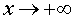не существует), нужно совершить 2 операции.

Первая операция. Вычислим предел

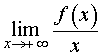(1)

Если предел (1) не существует или существует, но равен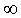, то делаем вывод о том, что у графика функции   y = f (x)   при 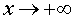наклонных асимптот нет.

Если предел (1) существует и равен некоторому числу, то, обозначив это число буквой   k ,  

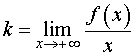
переходим ко второй операции.

Вторая операция. Вычислим предел

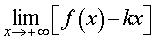(2)

Если предел (2) не существует или существует, но равен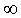, то делаем вывод о том, что у графика функции   y = f (x)   при 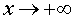наклонных асимптот нет.

Если предел (2) существует и равен некоторому числу, то, обозначив это число буквой   b ,

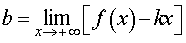
делаем вывод о том, что прямая

y = kx + b

является наклонной асимптотой графика функции   y = f (x)   при .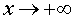

Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции   y = f (x)   при 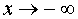(или убедиться, что наклонной асимптоты при 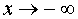не существует).

Первая операция. Вычислим предел

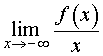(3)

Если предел (3) не существует или существует, но равен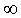, то делаем вывод о том, что у графика функции   y = f (x)   при 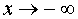наклонных асимптот нет.

Если предел (3) существует и равен некоторому числу, то, обозначив это число буквой   k ,

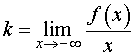
переходим ко второй операции.

Вторая операция. Вычислим предел

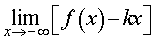(4)

Если предел (4) не существует или существует, но равен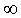, то делаем вывод о том, что у графика функции   y = f (x)   при 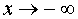наклонных асимптот нет.

Если предел (4) существует и равен некоторому числу, то, обозначив это число буквой   b ,

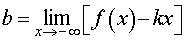
делаем вывод о том, что прямая

y = kx + b

является наклонной асимптотой графика функции   y = f (x)   при .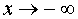

ПРИМЕР 5. Найти асимптоты графика функции

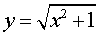(5)

и построить график этой функции.

РЕШЕНИЕ. Функция (5) определена для всех 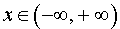и вертикальных асимптот не имеет.

Найдем наклонные асимптоты графика функции (5). При 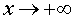получаем

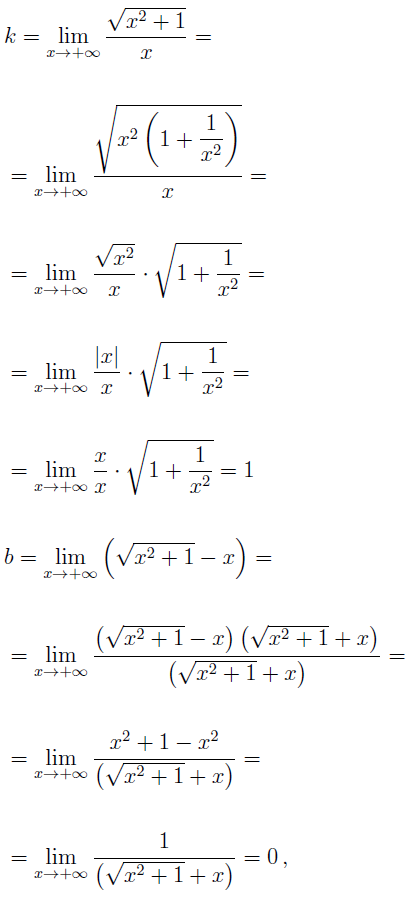
Отсюда вытекает, что прямая

y = x

– наклонная асимптота графика функции (5) при .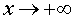

При 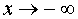получаем

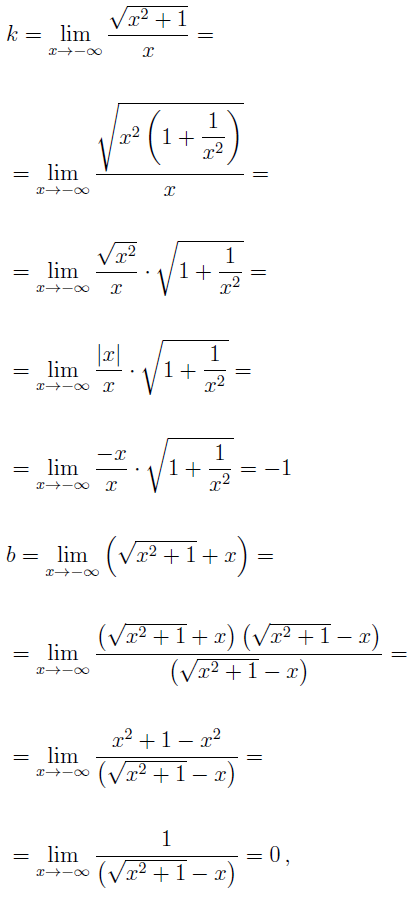
Отсюда вытекает, что прямая

y = – x

– наклонная асимптота графика функции (5) при .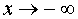

Функция (5) является четной функцией, поэтому ее график симметричен относительно оси ординат.

Найдем производную функции (5):

.

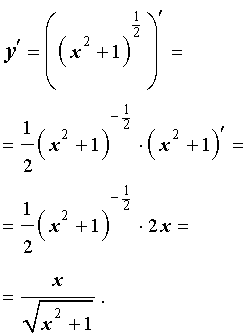Итак,   y' > 0   при   x > 0 ,   y' < 0   при   x < 0 ,   y' = 0   при   x = 0 .   Точка   x = 0   – стационарная, причем производная функции (5) при переходе через точку   x = 0   меняет знак с   «–»   на   «+» . Следовательно,   x = 0   – точка минимума функции (5). Других критических точек у функции (5) нет.

Теперь мы уже можем построить график функции (5):

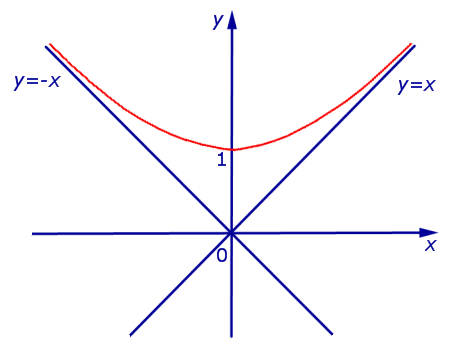
Рис.6

Заметим, что график функции (5) находится выше асимптот   y = x   и   y =– x ,   поскольку справедливо неравенство:

.

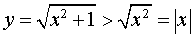Близкие по тематике разделы сайта

С материалами, связанными со свойствами функций и их пределами, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»

Примеры построения графиков функций и, в частности, с примеры поиска асимптот графика функции, можно посмотреть в учебных пособиях:

• «Исследование функций с помощью производных. Построение графиков (часть 1)»
• «Исследование функций с помощью производных. Построение графиков (часть 2)»

на странице  «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».