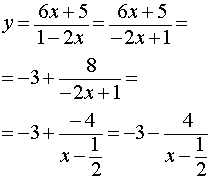Гипербола на координатной плоскости.
График дробно-линейной функции
 Гипербола на координатной плоскости Гипербола на координатной плоскости |
 Примеры графиков дробно-линейных функций Примеры графиков дробно-линейных функций |
Гипербола на координатной плоскости
Определение 1. Гиперболой (равносторонней гиперболой) называют график функции
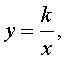 | (1) |
где k – любое, отличное от нуля, число.
Функция (1) обладает следующими свойствами:
- областью определения функции (1) является вся числовая ось за исключением точки x = 0, в которой знаменатель обращается в нуль;
- функция (1) является нечетной функцией, поскольку для всех значений аргумента выполнено равенство
- при k > 0 функция (1) убывает на интервале
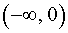 и на интервале
и на интервале 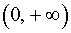 ;
;
при k < 0 функция возрастает на интервале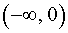 и на интервале
и на интервале 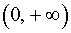 ;
; - прямая x = 0 является вертикальной асимптотой графика функции (1), так как в формуле (1) при x = 0 знаменатель обращается в нуль;
- прямая y = 0 является горизонтальной асимптотой графика функции (1), так как в формуле (1) дробь (1) стремится к нулю, когда знаменатель стремится в бесконечность дробь (1) стремится к нулю, когда знаменатель стремится в бесконечность.
y (x) = – y (– x) ;
Рассмотрим теперь функцию, заданную формулой
| (2) |
где a, b, c, d – произвольные числа, а число c не равно нулю.
Определение 2. Дробно-линейной функцией называют функцию, заданную формулой (2), если дробь, стоящая в правой части формулы (2), несократима.
Графиком дробно–линейной функции является гипербола.
Примеры графиков дробно–линейных функций
| Функция | График |
x = 0, y = 0. |
|
x = 0, y = 0. |
|
x = 2, y = 0. |
|
x = 2, y = 0. |
|
x = – 2, y = 0. |
|
x = – 1, y = 3. |
|
x = – 1, y = – 3. |
|
|
|
Функция:
x = 0, y = 0. График: 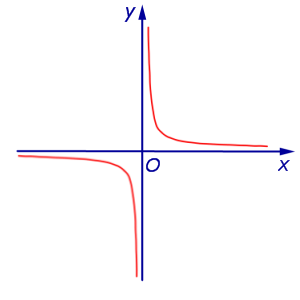 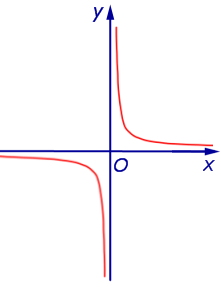 |
Функция:
x = 0, y = 0. График: 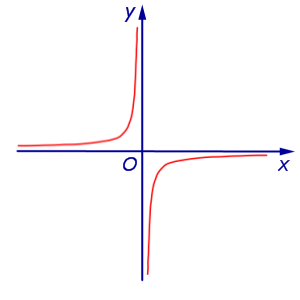 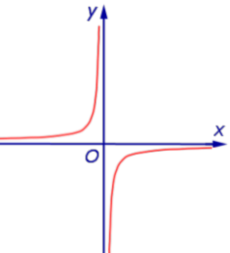 |
Функция:
x = 2, y = 0. График: 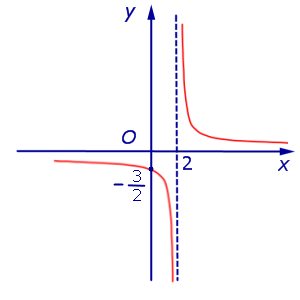 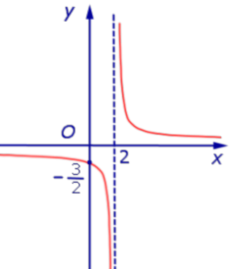 |
Функция:
x = 2, y = 0. График: 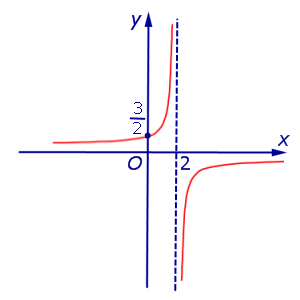 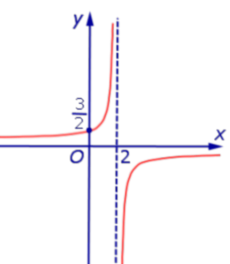 |
Функция:
x = – 2, y = 0. График: 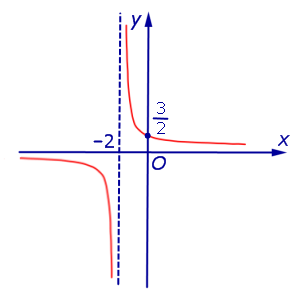 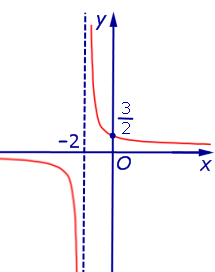 |
Функция:
x = – 1, y = 3. График: 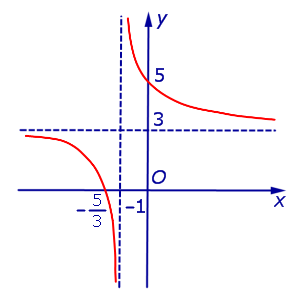 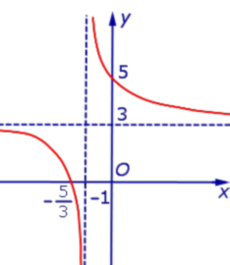 |
Функция:
x = – 1, y = – 3. График: 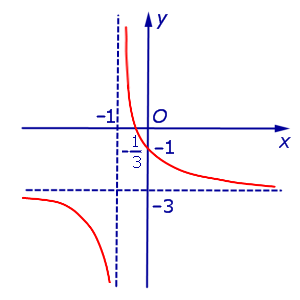 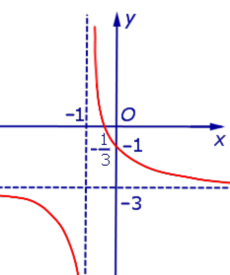 |
Функция:
График: 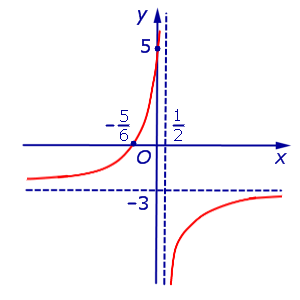 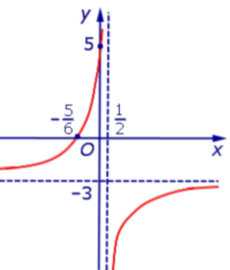 |

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |