На этой странице нашего сайта размещены учебно-методические пособия по математическому анализу (1курс, 2 семестр), которые использовались при проведении семинарских занятий со студентами МФТИ. Курс математического анализа, читаемый студентам МФТИ во 2 семестре, называется «Многомерный анализ, интегралы и ряды».
Каждое из учебно-методических пособий содержит теоретические сведения и примеры решения типовых задач по изучаемому разделу математического анализа. Практически все разобранные в учебно-методических пособиях задачи ранее предлагались для решения студентам МФТИ в заданиях для самостоятельной работы, на семестровых контрольных работах и на устных экзаменах по математическому анализу во 2 семестре. В справочной форме приводится необходимая для решения задач теория.
Мы надеемся, что эти учебные материалы будут полезными не только студентам МФТИ, осваивающим курс математического анализа, но и студентам других ВУЗов.
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Открытые и замкнутые множества в Rn
В пособии изучаются простейшие свойства открытых и замкнутых множеств n - мерных евклидовых пространствах Rn.
Содержание
- Внутренние точки множества. Открытые множества.
- Линейно связные множества. Области.
- Точки прикосновения. Предельные точки. Изолированные точки. Граничные точки. Граница множества.
- Замкнутые множества.
Перейти к учебному пособию «Открытые и замкнутые множества в Rn»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Неопределенный интеграл. Простейшие приемы интегрирования
В пособии рассматриваются методы вычисления неопределенных интегралов с помощью замены переменной и интегрирования по частям. Решаются типовые примеры из студенческих домашних заданий и экзаменационных контрольных работ.
Содержание
- Первообразная.
- Неопределенный интеграл.
- Табличные интегралы.
- Вычисление простейших интегралов.
- Вычисление интегралов при помощи замены переменной.
- Вычисление интегралов при помощи интегрирования по частям.
- Задачи на вычисление интегралов из экзаменационных контрольных работ.
Перейти к учебному пособию «Неопределенный интеграл. Простейшие приемы интегрирования»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Интегрирование рациональных дробей
В пособии рассматриваются методы вычисления неопределенных интегралов от рациональных дробей при помощи разложения рациональных дробей на простейшие дроби. Приводится схема вычисления интегралов от рациональных дробей. Решаются типовые примеры из студенческих домашних заданий и экзаменационных контрольных работ.
Перейти к учебному пособию «Интегрирование рациональных дробей»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Интегрирование иррациональных функций
Пособие посвящено методам вычисления неопределенных интегралов от иррациональных функций. Основу этих методов составляет поиск подходящих замен переменной, позволяющих свести интегралы от иррациональных функций к интегралам от рациональных дробей. Рассматриваются подстановки Эйлера и подстановки, с помощью которых можно проинтегрировать дифференциальный бином. Решаются типовые примеры из студенческих домашних заданий и экзаменационных контрольных работ.
Содержание
- Интегрирование иррациональных функций, содержащих корни из дробно-линейного выражения.
- Интегрирование иррациональных функций, содержащих квадратный корень из квадратного трехчлена. Подстановки Эйлера.
- Интегрирование дифференциального бинома.
Перейти к учебному пособию «Интегрирование иррациональных функций»
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Интегрирование выражений, содержащих тригонометрические и гиперболические функции
В пособии рассматриваются методы интегрирования выражений, содержащих тригонометрические и гиперболические функции. Решаются типовые примеры из студенческих домашних заданий и экзаменационных контрольных работ.
Содержание
- Универсальная тригонометрическая подстановка.
- Вычисление интегралов вида
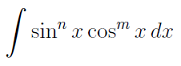
- Вычисление интегралов вида
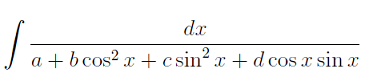
- Вычисление интегралов вида
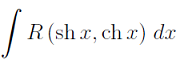
- Применение тригонометрических и гиперболических подстановок для вычисления интегралов от рациональных дробей и иррациональных функций.
Самарова С.С.
Учебное пособие для студентов МФТИ по математике
Предел и непрерывность функций двух переменных
В пособии рассматриваются двойные пределы, повторные пределы и пределы по направлениям, а также понятия непрерывности и равномерной непрерывности функций двух переменных.
Содержание
- Двойной предел функций двух переменных.
- Предел функции двух переменных по направлению.
- Повторные пределы.
- Непрерывность функции двух переменных.
- Равномерная непрерывность функции двух переменных.
Перейти к учебному пособию «Предел и непрерывность функций двух переменных»
Близкие по тематике разделы сайта
С материалами, связанными с вычислением неопределенных и определенных интегралов, а также с геометрическими приложениями определенных интегралов, можно ознакомиться в разделе нашего справочника: «Интегралы» и в учебном пособии «Интегральное исчисление функций одной переменной»