Справочник по математикеЭлементы математического анализа Производная функции

Построение графиков функций

Содержание

	Схема исследования поведения функций, применяемая для построения графиков функций
	Примеры построения графиков функций

Схема исследования поведения функций, применяемая для построения графиков функций

Для построения графика функции   y = f (x)   желательно сначала провести исследование поведения функции   y = f (x)   по следующей схеме.

1. Найти область определения   D ( f ).

2. Выяснить, является ли функция   y = f (x)   четной или нечетной.

3. Выяснить, является ли функция   y = f (x)  периодической.

4. Найти асимптоты графика функции.

5. Вычислить производную функции   f ' (x) .

6. Найти критические точки функции   y = f (x) .

7. Найти интервалы возрастания и убывания функции   y = f (x) .

8. Найти экстремумы функции   y = f (x) .

9. Найти точки пересечения графика функции   y = f (x)   с осями координат.

   Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс   Ox,   то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.

10. Вычислить вторую производную функции   f "  (x) .

11. Найти интервалы, на которых функция   y = f (x)   выпукла вверх, а также интервалы, на которых функция   y = f (x)  выпукла вниз.

12. Найти точки перегиба графика функции  y = f (x) .

ЗАМЕЧАНИЕ. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.

Примеры построения графиков функций

ПРИМЕР 1. Построить график функции

РЕШЕНИЕ. Областью определения функции (1) является вся числовая прямая.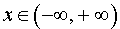

Функция (1) не является ни четной, ни нечетной.

Функция (1) не является периодической.

Вертикальных асимптот у графика функции (1) нет, так как для любого числа   x₀

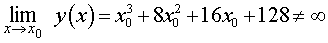
Проверим, есть ли у графика функции (1) наклонные асимптоты. Поскольку

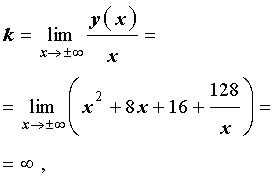
то делаем вывод, что наклонных асимптот у графика функции (1) нет.

Теперь вычислим производную функции (1):

y' (x) = 3x² + 16x + 16 .

Поскольку   y' (x)   существует для всех 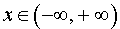, то все критические точки функции являются ее стационарными точками, то есть точками, в которых

y' (x) = 0 .

Найдем стационарные точки функции (1), интервалы, на которых   y' (x)   сохраняет знак, а также экстремумы функции. Для этого решим квадратное уравнение

3x² + 16x + 16 = 0.

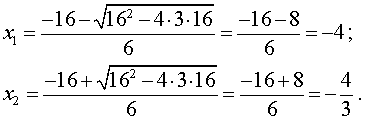
Изобразим на рисунке 1 диаграмму знаков производной   y' (x)

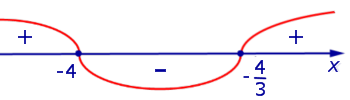
Рис.1

На интервалах 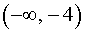и 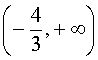производная   y' (x)   положительна, значит, функция (1) возрастает. На интервале 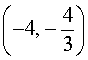производная   y' (x)   отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.

Рис.2

При переходе через точку   x = – 4   производная функции   y' (x)   меняет знак с   «+»   на   «–» . Следовательно, точка   x = – 4   является точкой максимума функции (1). При переходе через точку 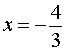производная функции   y' (x)   меняет знак с   «–»   на   «+» . Следовательно, точка 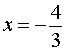является точкой минимума функции (1).

Найдем значения функции (1) в стационарных точках:

y (–4) = 256 ,

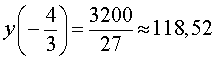
Теперь вычислим вторую производную функции (1):

y" (x) = (y' (x))' =

= (3x² + 16x + 16)' =

= 6x + 16 .

Вторая производная   y" (x)   обращается в нуль при 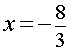. Изобразим на рисунке 3 диаграмму знаков второй производной   y" (x)

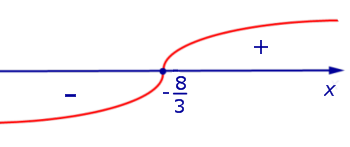
Рис.3

При переходе через точку 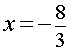вторая производная функции   y" (x)   меняет знак с   «–»   на   «+» . Следовательно, 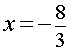– точка перегиба графика функции (1). При 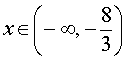функция (1) выпукла вверх, при 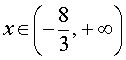функция (1) выпукла вниз.

Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).

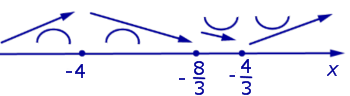
Рис.4

Для того, чтобы найти точки пересечения функции (1) с осью   Ox ,   решим уравнение

x³ + 8x² + 16x + 128 = 0 ,

x² (x + 8) + 16 (x + 8) = 0 ,

(x + 8) (x² + 16) = 0 .

Таким образом, точка   (– 8; 0)   является единственной точкой пересечения графика функции (1) с осью   Ox .   Точкой пересечения графика функции (1) с осью   Oy   будет точка   (0; 128) .

На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).

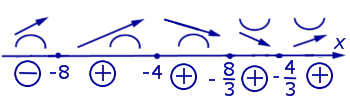
Рис.5

Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис.6):

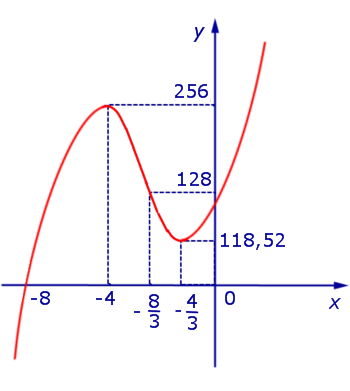
Рис.6

ПРИМЕР 2. Построить график функции

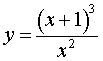(2)

РЕШЕНИЕ. Областью определения функции (2) является вся числовая прямая, за исключением точки   x = 0 ,   то есть

.

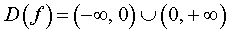Функция (2) не является ни четной, ни нечетной.

Функция (2) не является периодической.

Прямая   x = 0   является вертикальной асимптотой графика функции (2), так как

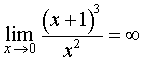
Для того, чтобы выяснить, имеются ли у графика функции (2) наклонные асимптоты, представим правую часть формулы (2) в другом виде:

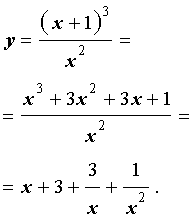(3)

Из формулы (3) получаем равенство

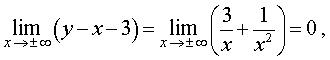
откуда вытекает, что прямая

y = x + 3

является наклонной асимптотой графика функции (2), как при 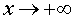, так и при .

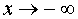Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):

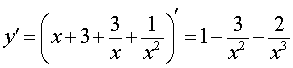(4)

Для того, чтобы найти стационарные точки функции (2), преобразуем правую часть формулы (4):

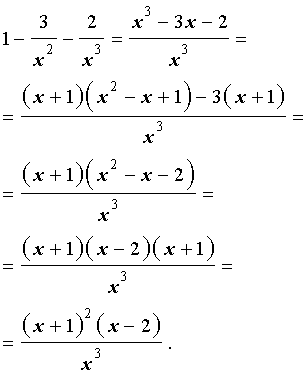
Следовательно,

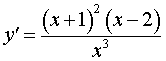(5)

и стационарными точками функции (2) являются точки   x = – 1   и   x = 2 .

Изобразим на рисунке 7 диаграмму знаков производной   y' (x)

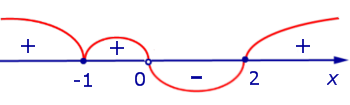
Рис.7

На интервалах 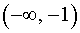, 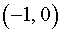и 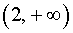производная   y' (x)   положительна, значит, функция (2) возрастает на этих интервалах. На интервале   (0, 2)   производная   y' (x)   отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.

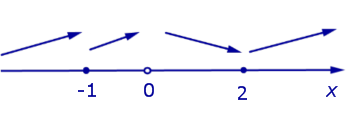
Рис.8

При переходе через точку   x = – 1   производная функции   y' (x)   знак не меняет, значит, в этой точке экстремума нет. При переходе через точку   x = 2   производная функции   y' (x)   меняет знак с   «–»   на   «+» .   Следовательно, точка   x = 2   является точкой минимума функции (2).

Найдем значения функции (1) в стационарных точках:

y (–1) = 0 ,

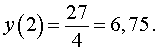
Теперь перейдем к вычислению второй производной функции (2). Проще всего это сделать, воспользовавшись формулой (4):

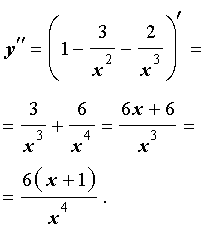
Вторая производная   y" (x)   обращается в нуль при   x = – 1 .   Изобразим на рисунке 9 диаграмму знаков второй производной   y" (x)

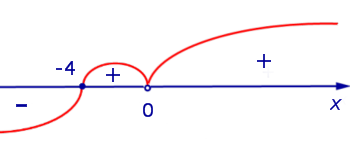
Рис.9

При переходе через точку   x = – 1   вторая производная функции   y" (x)   меняет знак с   «–»   на   «+» . Следовательно,   x = – 1   – точка перегиба графика функции (2). При   x < – 1   функция (2) выпукла вверх, при   x > – 1   функция (2) выпукла вниз.

Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).

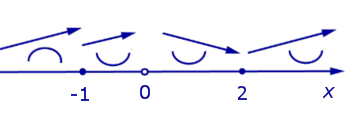
Рис.10

Найдем точки пересечения функции (2) с осями координат: точка   (– 1; 0)   является единственной точкой пересечения графика функции (2) с осью   Ox ,   а точек пересечения графика функции (2) с осью   Oy   нет, поскольку   x = 0   не входит в область определения функции (2).

На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).

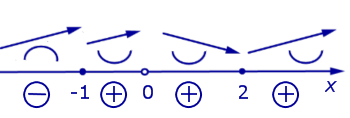
Рис.11

Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис.12):

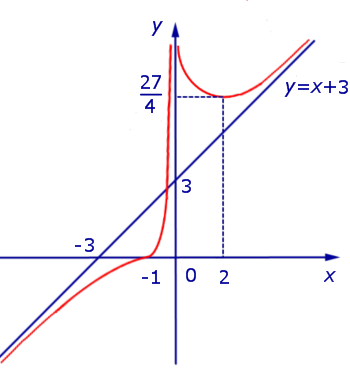
Рис.12

Близкие по тематике разделы сайта

С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»

Примеры построения графиков функций можно посмотреть в учебных пособиях:

• «Исследование функций с помощью производных. Построение графиков (часть 1)»
• «Исследование функций с помощью производных. Построение графиков (часть 2)»

на странице  «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».