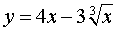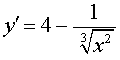Справочник по математике
Элементы математического анализа Производная функции
Наибольшее и наименьшее значения функции на отрезке
Содержание
 |
Наибольшее и наименьшее значения функции на множестве (основные определения) |
|
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса |
|
Примеры решения задач |
Наибольшее и наименьшее значения функции на множестве (основные определения)
Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x).
ОПРЕДЕЛЕНИЕ 1. Значение f (x0) функции y = f (x) в точке
называют наибольшим значением функции f (x) на множестве X, если для любой точки 
выполнено неравенство
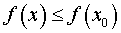
Наибольшее значение функции f (x) на множестве X часто обозначают
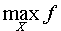или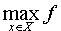 
ОПРЕДЕЛЕНИЕ 2. Значение f (x0) функции y = f (x) в точке 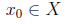называют наименьшим значением функции f (x) на множестве X, если для любой точки 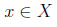выполнено неравенство
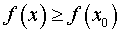
Наименьшее значение функции f (x) на множестве X часто обозначают
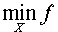или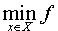 
ОПРЕДЕЛЕНИЕ 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .
ПРИМЕР 1. Минимальным значением функции y = x2 на множестве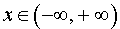 
является число 0 (рис. 1).
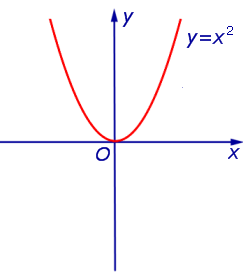
Рис.1
Максимального значения функция y = x2 на множестве 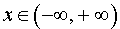не имеет.
ПРИМЕР 2. Максимальным значением функции y = – x2 на множестве 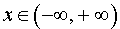является число 0 (рис. 2).
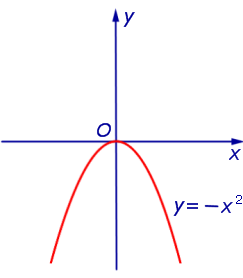
Рис.2
Минимального значения функция y = – x2 на множестве 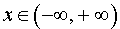не имеет.
ПРИМЕР 3. Функция y = x на множестве 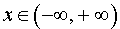не имеет ни максимального, ни минимального значений (рис. 3).
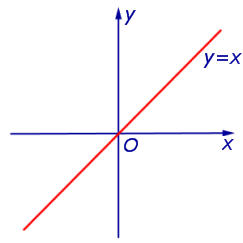
Рис.3
ПРИМЕР 4. Функция y = arctg x на множестве 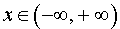не имеет ни максимального, ни минимального значений (рис. 4).
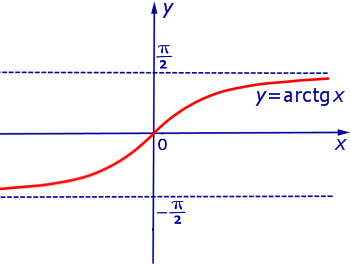
Рис.4
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса
Как мы видели в примерах 1 - 4, даже такие хорошо известные функции, как
y = x2, y = – x2, y = x, y = arctg x
не имеют наибольших или наименьших значений на множестве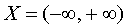
. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.
ТЕОРЕМА ВЕЙЕРШТРАССА. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.
Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.
СЛЕДСТВИЕ. Пусть x1 , x2 , ... , xn – критические точки функции y = f (x) на отрезке [a, b] . Тогда наибольшее и наименьшее значения функции y = f (x) на отрезке [a, b] равны наибольшему и наименьшему из чисел
f (a) , f (b) , f (x1) , f (x2) , ... , f (xn)
соответственно.
Примеры решения задач
ЗАДАЧА 1. Найти наибольшее и наименьшее значения функции
| y = 2x3 + 3x2 – 36x + 30 | (1) |
на отрезке [–2, 4] .
РЕШЕНИЕ. Найдем критические точки функции (1). Для этого вычислим производную функции (1):
|
y' = 6x2 + 6x – 36 = |
(2) |
Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:
y (2) = – 14 , y (– 2) = 98 , y (4) = 62 .
ОТВЕТ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наименьшее значение функции (1) на отрезке [–2, 4] равно – 14 .
ЗАДАЧА 2. Найти наибольшее и наименьшее значения функции
|
|
(3) |
на отрезке [–1, 27] .
РЕШЕНИЕ. Найдем критические точки функции (3). Для этого вычислим производную функции (3):
|
|
(4) |
Решая уравнение y' = 0 , получим
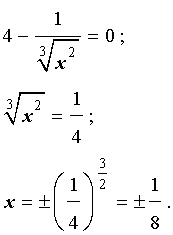
Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0,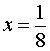 
и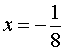 
, причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, 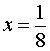и 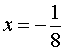, а также на концах отрезка x = – 1 и x = 27 , получим:
y (0) = 0 ,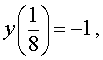 
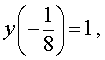y (– 1) = – 1 , y (27) = 99 .
ОТВЕТ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наименьшее значение функции (3) на отрезке [–1, 27] равно – 1 .
ЗАДАЧА 3. Найти наибольшее и наименьшее значения функции
|
y = (x – 4) e| x | |
(5) |
на отрезке [–1, 6] .
РЕШЕНИЕ. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:
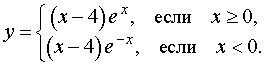
Следовательно,
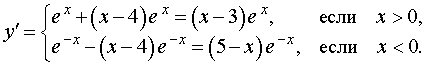
В точке x = 0 производная функции (5) не существует. Критическими точками являются точки
x = 0, x = 3, x = 5.
Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:
y (0) = – 4 , y (3) = – e 3, y (5) = e 5, y (– 1) = – 5e , y (6) = 2e 6.
ОТВЕТ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6, а наименьшее значение функции (5) на отрезке [–1, 6] равно – e 3.
ЗАДАЧА 4. Найти наибольшее значение функции
|
y = (x – 27) e 28 – x |
(6) |
на отрезке [23, 40] .
РЕШЕНИЕ. Найдем критические точки функции (6). Для этого вычислим производную функции (6):
|
y' = e 28 – x – (x – 27) e 28 – x = |
(7) |
Решая уравнение y' = 0 , получаем, что функция (6) имеет единственную критическую точку x = 28 , причем эта точка лежит на отрезке [23, 40] . При переходе через точку x = 28 производная функции (7) меняет знак с «+» на «–» , откуда вытекает, что точка x = 28 является точкой максимума функции (6) на множестве 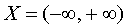. Следовательно, точка x = 28 является точкой максимума функции (6) и на отрезке [23, 40] . Найдем значение функции (6) в точке x = 28:
y (28) = 1 .
ОТВЕТ. Наибольшее значение функции (6) на отрезке [23, 40] равно 1.
Близкие по тематике разделы сайта
С материалами, связанными с дифференцированием функций и применением производных к исследованию поведения функций, можно также ознакомиться в учебном пособии «Дифференциальное исчисление функций одной переменной»
Примеры построения графиков функций можно посмотреть в учебных пособиях:
- «Исследование функций с помощью производных. Построение графиков (часть 1)»
- «Исследование функций с помощью производных. Построение графиков (часть 2)»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 1 семестр)».