Справочник по математике Тригонометрия
Тригонометрия
Основные тригонометрические формулы
Содержание

Связи между тригонометрическими функциями одного угла
| sin2α + cos2α = 1 |
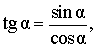 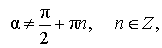 |
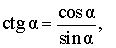 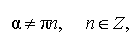 |
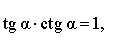 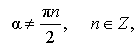 |
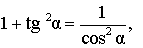 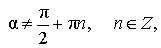 |
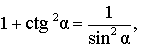 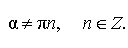 |
Тригонометрические функции суммы и разности двух углов
| Синус суммы |
| sin (α + β) = sin α cos β + cos α sin β |
| Синус разности |
| sin (α – β) = sin α cos β – cos α sin β |
| Косинус суммы |
| cos (α + β) = cos α cos β – sin α sin β |
| Косинус разности |
| cos (α – β) = cos α cos β + sin α sin β |
| Тангенс суммы |
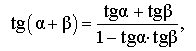 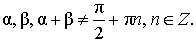 |
| Тангенс разности |
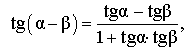 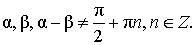 |
Тригонометрические функции двойного угла
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
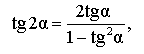 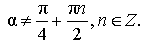 |
Формулы понижения степени для квадратов тригонометрических функций
| Выражение квадрата синуса через косинус двойного угла |
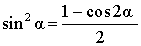 |
| Выражение квадрата косинуса через косинус двойного угла |
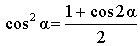 |
| Выражение квадрата тангенса через косинус двойного угла |
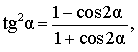 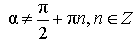 |
Формулы понижения степени для кубов синуса и косинуса
| Выражение куба синуса через синус угла и синус тройного угла |
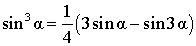 |
| Выражение куба косинуса через косинус угла и косинус тройного угла |
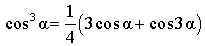 |
Выражение тангенса через синус и косинус двойного угла
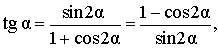 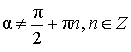 |
Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
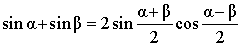 |
| Разность синусов |
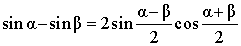 |
| Сумма косинусов |
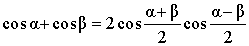 |
| Разность косинусов |
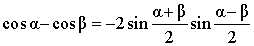 |
| Сумма тангенсов |
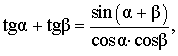 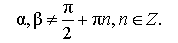 |
| Разность тангенсов |
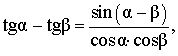 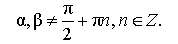 |
Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
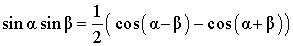 |
| Произведение косинусов |
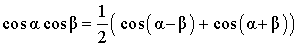 |
| Произведение синуса и косинуса |
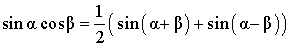 |
Выражение тригонометрических функций через тангенс половинного угла
| Выражение синуса угла через тангенс половинного угла |
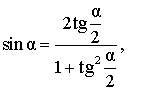 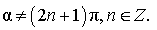 |
| Выражение косинуса угла через тангенс половинного угла |
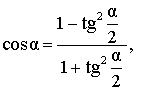 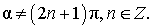 |
| Выражение тангенса угла через тангенс половинного угла |
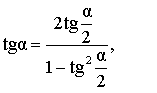 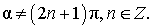 |
Тригонометрические функции тройного угла
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
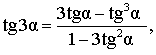 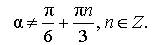 |

