Справочник по математике
Тригонометрия
Измерение углов. Градусы и радианы
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.
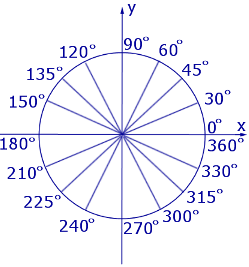
Рис.1
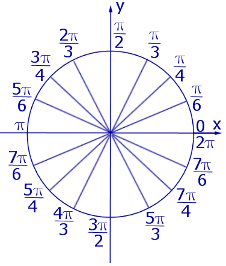
Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий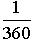 
полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
СЛЕДСТВИЕ 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
СЛЕДСТВИЕ 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
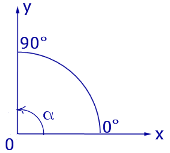
Рис.3
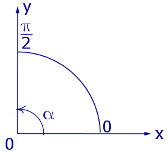
Рис.4
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен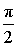 
радиан. Следовательно,
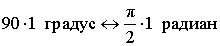
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид
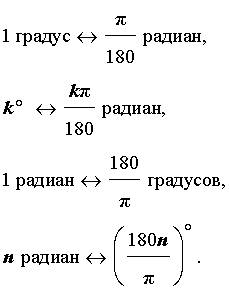
Поскольку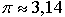 
, то
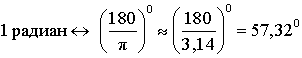
По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.
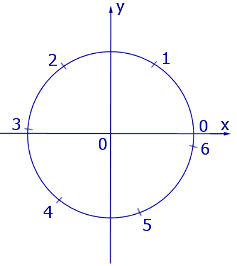
Рис.5
ЗАМЕЧАНИЕ. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
ПРИМЕР. Найти наименьшее из чисел:
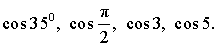
РЕШЕНИЕ. Поскольку
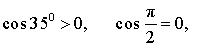
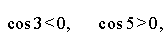
то наименьшим числом является число cos 3 .