Справочник по математикеТригонометрия

Значения тригонометрических функций

Содержание

	Таблица значений тригонометрических функций часто используемых углов
	Вычисление значений тригонометрических функций

Таблица значений тригонометрических функций часто используемых углов

I   четверть
α (рад):  0,   – 2π α (град): 0°,   – 360°
sin α	0
cos α	1
tg α	0
ctg α	не существует
α (рад): 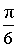  , 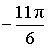   α (град): 30°,   – 330°
sin α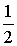
cos α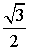
tg α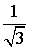
ctg α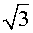
α (рад): 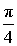  , 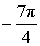   α (град): 45°,   – 315°
sin α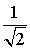
cos α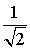
tg α	1
ctg α	1
α (рад): 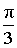  , 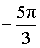   α (град): 60°,   – 300°
sin α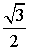
cos α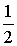
tg α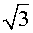
ctg α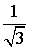
α (рад): 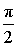  , 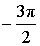   α (град): 90°,   – 270°
sin α	1
cos α	0
tg α	не существует
ctg α	0
II  четверть
α (рад): 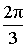  , 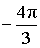   α (град): 120°,   – 240°
sin α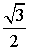
cos α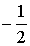
tg α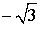
ctg α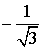
α (рад): 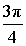  , 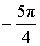   α (град): 135°,   – 225°
sin α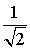
cos α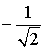
tg α	– 1
ctg α	– 1
α (рад): 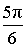  , 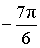   α (град): 150°,   – 210°
sin α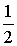
cos α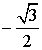
tg α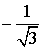
ctg α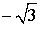
α (рад):   π,   – π α (град): 180°,   – 180°
sin α	0
cos α	– 1
tg α	0
ctg α	не существует
III  четверть
α (рад): 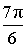  , 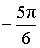   α (град): 210°,   – 150°
sin α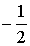
cos α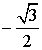
tg α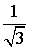
ctg α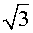
α (рад): 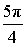  , 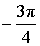   α (град): 225°,   – 135°
sin α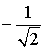
cos α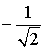
tg α	1
ctg α	1
α (рад): 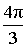  , 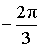   α (град): 240°,   –120°
sin α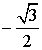
cos α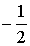
tg α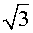
ctg α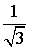
α (рад): 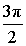  , 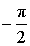  α (град): 270°,   – 90°
sin α	– 1
cos α	0
tg α	не существует
ctg α	0
IV  четверть
α (рад): 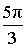  , 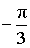   α (град): 300°,   – 60°
sin α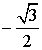
cos α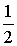
tg α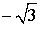
ctg α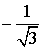
α (рад): 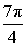  , 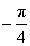   α (град): 315°,   – 45°
sin α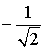
cos α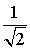
tg α	– 1
ctg α	– 1
α (рад): 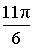  , 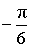   α (град): 330°,   –30°
sin α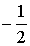
cos α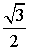
tg α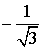
ctg α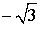
α (рад):   2π,  0 α (град): 360°,   0°
sin α	0
cos α	1
tg α	0
ctg α	не существует

Примеры вычисления значений тригонометрических функций

ПРИМЕР 1. Найти    sin 15°.

РЕШЕНИЕ. Воспользовавшись формулой «Синус разности», получаем:

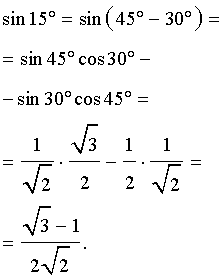
ПРИМЕР 2. Найти    cos 22,5°.

РЕШЕНИЕ. Воспользовавшись формулой «Косинус двойного угла», получаем:

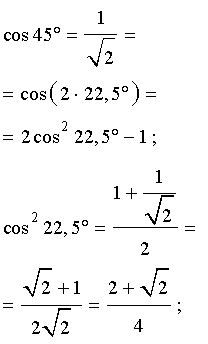
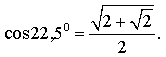
ПРИМЕР 3. Найти    sin 18°.

РЕШЕНИЕ. Поскольку

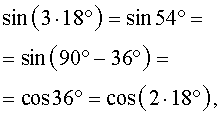
то, с помощью формул «Синус тройного угла» и «Косинус двойного угла», отсюда получаем:

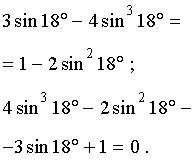
Теперь, если ввести обозначение

sin 18° = t ,

то возникает кубическое уравнение

4t³ – 2t² – 3t + 1 = 0 .

Решим это уравнение, раскладывая его левую часть на множители:

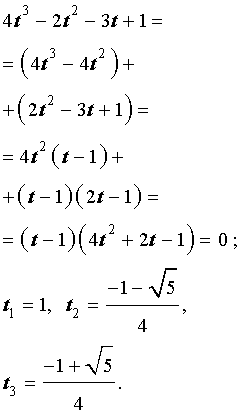
Поскольку

0 < sin 18° < 1 ,

то первый и второй корни должны быть отброшены. Следовательно,