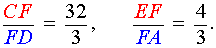Справочник по математикеГеометрия (Планиметрия) Треугольники

Теорема Менелая

ТЕОРЕМА МЕНЕЛАЯ 1. Если на сторонах AB и BC треугольника ABC взяты соответственно точки C₁ и A₁, а точка B₁ взята на продолжении стороны AC за точку C (рис.1), то точки C₁, A₁ и B₁ лежат на одной прямой тогда и только тогда, когда выполнено равенство

.

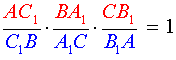(1)

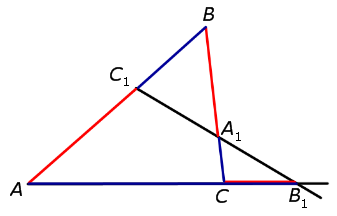
Рис.1

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ. Докажем, что если точки   C₁, A₁ и B₁ лежат на одной прямой, то выполнено равенство (1). Для этого проведём через точку C прямую, параллельную прямой AB, и обозначим буквой D её точку пересечения с прямой C₁B₁ (рис.2).

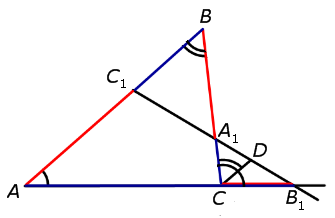
Рис.2

Поскольку треугольник AC₁B₁ подобен треугольнику CDB₁, то выполнено равенство

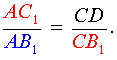(2)

Поскольку треугольник C₁BA₁ подобен треугольнику A₁DC, то выполнено равенство

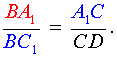(3)

Перемножая равенства (2) и (3), получим

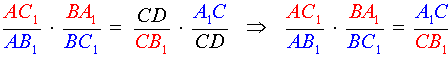
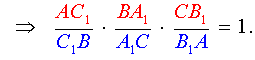
Доказательство необходимости завершено.

ДОКАЗАТЕЛЬСТВО ДОСТАТОЧНОСТИ. Докажем, что если выполнено равенство (1), то точки C₁, A₁ и   B₁ лежат на одной прямой.

Воспользуемся методом «от противного». С этой целью проведём прямую через точки C₁ и A₁ и обозначим символом B₂ точку пересечения этой прямой с прямой AC (рис. 3).

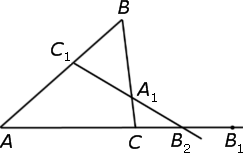
Рис.3

Поскольку точки C₁, A₁ и B₂ лежат на одной прямой, то выполнено равенство

.

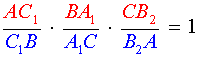(4)

Кроме того, выполнено равенство (1)

.

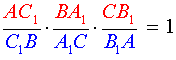(1)

Разделив равенство (4) на равенство (1), получим равенство

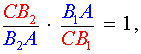
следствием которого является равенство

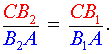(5)

Воспользовавшись свойствами производных пропорций, из равенства (5) получаем, что точки B₁  и B₂ совпадают.

Доказательство достаточности завершено.

Теорема Менелая 1 доказана.

ЗАМЕЧАНИЕ. Если чуть-чуть изменить формулировку теоремы Менелая 1, выбрав точку B₁ на продолжении стороны AC за точку A (рис.4), то доказательство теоремы Менелая практически не изменится, и мы предоставляем его читателю в качестве упражнения.

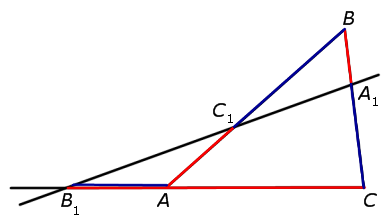
Рис.4

ТЕОРЕМА МЕНЕЛАЯ 2. Если на продолжениях сторон AB, BC и AC треугольника ABC взяты соответственно точки C₁, A₁ и B₁ (рис.5), то точки C₁, A₁ и B₁ лежат на одной прямой тогда и только тогда, когда выполнено равенство

.

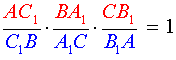(6)

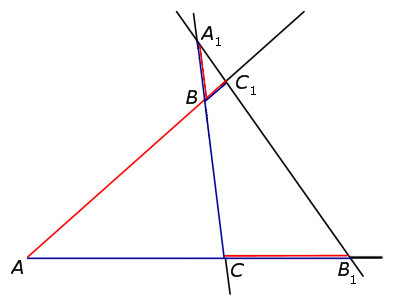
Рис.5

ЗАМЕЧАНИЕ. Доказательство теоремы Менелая 2 почти дословно повторяет доказательство теоремы Менелая 1, и мы оставляем его читателю в качестве упражнения.

Для того, чтобы показать, как можно применять теорему Менелая, решим следующую задачу.

ЗАДАЧА. На сторонах AB и BC треугольника ABC взяты точки D и E соответственно, причем

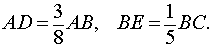
Отрезки AE и CD пересекаются в точке F (рис.6). В каком отношении отрезки AE и CD делятся точкой F?

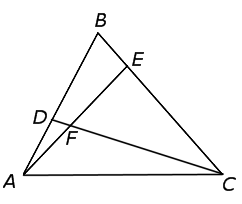
Рис.6

РЕШЕНИЕ. Применив к треугольнику BCD теорему Менелая (рис. 7),

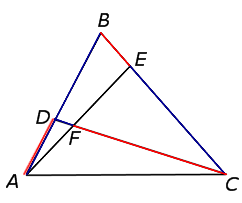
Рис.7

получим

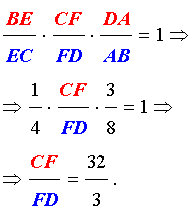
Применив к треугольнику ABE теорему Менелая (рис. 8),

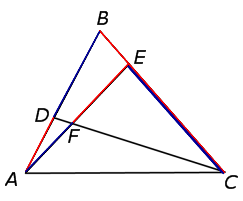
Рис.8

получим

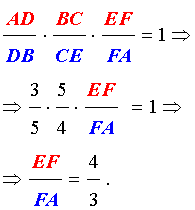
ОТВЕТ: