Справочник по математике
Арифметика Пропорции и пропорциональная зависимость
Пропорции, члены пропорции, основное свойство пропорции
Содержание
 |
Пропорции, члены пропорции. Основное свойство пропорции |
|
Производные пропорции |
|
Свойства равных отношений |
Пропорции, члены пропорции. Основное свойство пропорции
Частное от деления числа a на число b называют отношением числа a к числу b.
Число a называют предыдущим членом отношения, число b – последующим членом отношения.
Пропорцией называют равенство двух отношений:
.
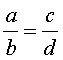Иногда пропорцию записывают так:
a : b = c : d .
И в одной, и во второй формах записи пропорции числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:
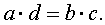
Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.
Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение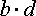 
.
В результате получим:
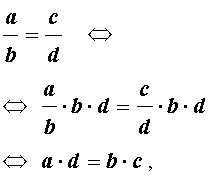
что и требовалось доказать.
Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.
ПРИМЕР 1. Найти неизвестный член пропорции x , если
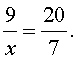
РЕШЕНИЕ. Воспользовавшись основным свойством пропорции, получаем:
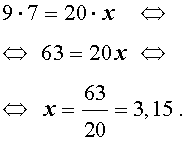
ОТВЕТ: 3,15 .
ПРИМЕР 2. Найти неизвестный член пропорции x , если
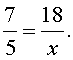
РЕШЕНИЕ. Воспользовавшись основным свойством пропорции, получаем:
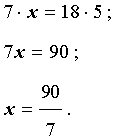
ОТВЕТ: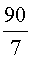 
.
Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если
.
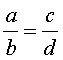то
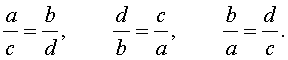
Производные пропорции
Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если
,
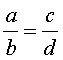то
|
 , |
|
 , |
|
 , |
|
 , |
|
 , |
|
 |
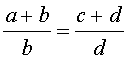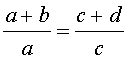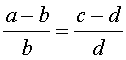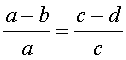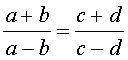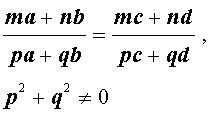В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции
.
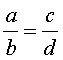достаточно прибавить 1. В результате получаем,
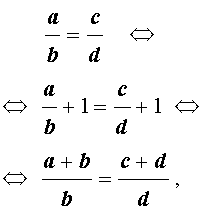
что и требовалось.
ЗАМЕЧАНИЕ. Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.
Свойства равных отношений
Если выполнено соотношение
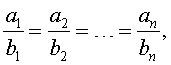
то выполнено и соотношение
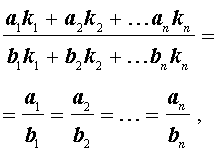
где
k1 , k2 , … kn
– произвольные числа, которые не могут все одновременно равняться нулю.