Справочник по математике
Арифметика Пропорции и пропорциональная зависимость
Прямо пропорциональные величины, обратно пропорциональные величины
ОПРЕДЕЛЕНИЕ 1. Две величины y и x , связанные зависимостью
y = kx ,
где k – некоторое число, называются прямо пропорциональными. Число k называется коэффициентом прямой пропорциональности.
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график прямо пропорциональной зависимости имеет следующий вид
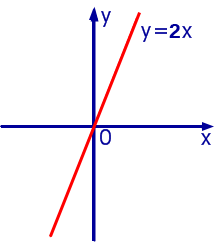
Отношение прямо пропорциональных величин является постоянным числом и равно k :
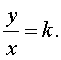
ОПРЕДЕЛЕНИЕ 2. Две величины y и x , связанные зависимостью
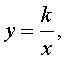
где k – некоторое число, называются обратно пропорциональными. Число k называется коэффициентом обратной пропорциональности.
Графиком обратно пропорциональной зависимости величин является гипербола.
Например, при k = 2 график обратно пропорциональной зависимости имеет следующий вид
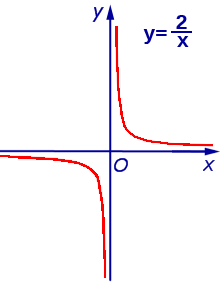
Произведение обратно пропорциональных величин является постоянным числом и равно k :
yx = k .
ПРИМЕР 1. Число 110 разделить на три слагаемых прямо пропорционально числам 1, 3 и 7 .
РЕШЕНИЕ. Если обозначить слагаемые буквами a , b и c , а коэффициент прямой пропорциональности буквой k и воспользоваться тем, что отношение прямо пропорциональных величин является числом постоянным, то будут выполнены соотношения:
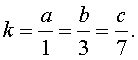
Следовательно,
b = 3a , c = 7a .
Поэтому
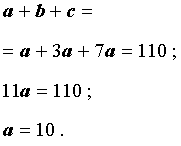
Таким образом,
b = 3a = 30, c = 7a = 70.
Итак, первое слагаемое равно 10 , второе слагаемое равно 30 , а третье слагаемое равно 70 . Их сумма равна 110 .
ОТВЕТ: 10 , 30 , 70 .
ПРИМЕР 2. Число 40 разделить на два слагаемых обратно пропорционально числам 1 и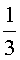 
.
РЕШЕНИЕ. Если обозначить слагаемые буквами a и b , а коэффициент обратной пропорциональности буквой k , и воспользоваться тем, что произведение обратно пропорциональных величин является числом постоянным, то будут выполнены соотношения:
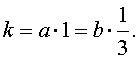
Следовательно:
b = 3a , a + b = 40, a + 3a = 40, 4a = 40, a = 10, b = 30.
Итак, первое слагаемое равно 10 , а второе слагаемое равно 30 . Их сумма равна 40 .
ОТВЕТ: 10 , 30 .