Справочник по математикеАрифметика Арифметика целых чисел

Целые числа. Десятичная система счисления

Содержание

	Натуральные (целые положительные) числа
	Целые отрицательные числа
	Целые числа
	Десятичная система счисления

Натуральные (целые положительные) числа

Числа

1 ,  2 ,  3 ,  …

называют натуральными или целыми положительными числами.

Множество натуральных чисел бесконечно. Множество натуральных чисел обозначают символом   N.

Число нуль, отрицательные и дробные числа не являются натуральными числами.

Целые отрицательные числа

Числа

– 1 ,  – 2 ,  – 3 ,  …

называют целыми отрицательными числами.

Множество целых отрицательных чисел бесконечно. Множество целых отрицательных чисел обозначают символом     N_– .

Целые числа

Множество целых чисел состоит из множества натуральных чисел, числа «нуль» и множества целых отрицательных чисел.

Множество целых чисел бесконечно. Множество целых чисел обозначают символом   Z . 

Десятичная система счисления

Системой счисления называют способ записи натуральных чисел при помощи символов, которые называют цифрами.

В обычной практической жизни используют десятичную система счисления. В этой системе числа записывают при помощи   10   цифр (арабских цифр):

0 ,  1 ,  2 ,  3 ,  4 ,  5 ,  6 ,  7 ,  8 ,  9 .

Например, число, десятичная запись которого  361 ,   равно сумме трёх сотен, шести десятков и одной единицы:

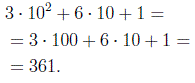
В данном справочнике мы рассматриваем только десятичную систему счисления.

ЗАДАЧА. Сумма квадратов цифр положительного двузначного числа равна   13 .   Если от этого числа отнять   9 ,   то получится число, записанное этими же цифрами, но в обратном порядке. Найдите это число.

РЕШЕНИЕ. Обозначив буквами   x   и   y   цифру десятков и цифру единиц искомого числа, соответственно, запишем это число в виде 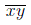    (черта сверху поставлена для того, чтобы отличить десятичную запись числа от произведения цифр   x   и   y).   Тогда:

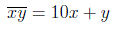
Число, записанное теми же цифрами, но в обратном порядке, имеет вид 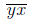  , причем

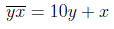
По условию задачи неизвестные   x   и   y   удовлетворяют системе уравнений

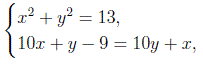
для решения которой преобразуем второе уравнение:

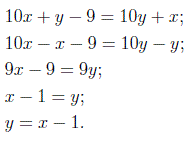
Далее получаем:

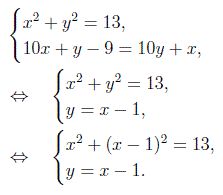
Теперь решим первое уравнение:

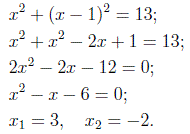
Поскольку число   – 2   не является цифрой, то второй корень должен быть отброшен. Следовательно,

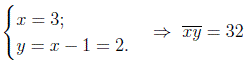
ОТВЕТ: Искомое число равно   32.