Справочник по математике
Арифметика Обыкновенные и десятичные дроби
Сравнение дробей
Содержание
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Например, из двух дробе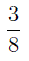й
и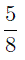 
большей является дробь с числителем 5.
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Например, из двух дробе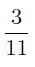й
и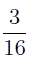 
большей является дробь со знаменателем 11 .
Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю
Для того, чтобы сравнить дроби с разными числителями и знаменателями, нужно сначала, пользуясь основным свойством дробей, привести их к соответственно равным дробям с одинаковыми знаменателями (привести к общему знаменателю), а затем сравнить полученные дроби, пользуясь методом сравнения дробей с одинаковыми знаменателями. Например, для того, чтобы сравнить дроб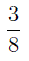и
и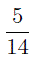 
,
приведем их к дробям с общим знаменателем, равным произведению знаменателей этих дробей:
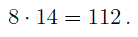
Тогда получим:
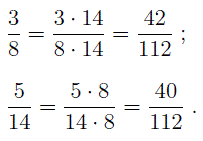
Следовательно, поскольку 42 > 40 , то
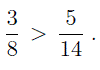
Приведение дробей к наименьшему общему знаменателю. Дополнительные множители
В разделе «Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю» мы сравнивали дроби при помощи их приведения к общему знаменателю, равному произведению знаменателей. Однако этот способ часто приводит к большим вычислениям. Иногда удается сократить вычисления, приводя дроби не просто к общему знаменателю, а к наименьшему общему знаменателю.
Например, для того, чтобы сравнить рассмотренные в разделе "Сравнение дробей с разными числителями и знаменателями. Приведение дробей к общему знаменателю" дроб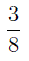и
и ,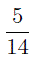
приведем их к дробям с наименьшим общим знаменателем, равным наименьшему общему кратному знаменателей этих дробей.
Наименьшим общим кратным чисел 8 и 14 является число 56 . Далее поскольку
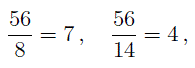
то
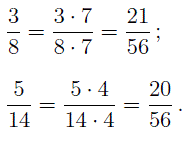
Так как 21 > 20 , то
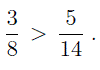
что и требовалось показать.
ЗАМЕЧАНИЕ. Числа 7 и 4 , полученные из формул
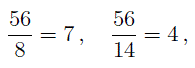
называют дополнительными множителями.