Справочник по математике Арифметика
Арифметика Проценты
Проценты
Проценты. Решение задач на проценты
ОПРЕДЕЛЕНИЕ. Одним процентом от числа a ( 1% от числа a ) называют число, равное
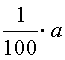
k процентами от числа a ( k % от числа a ) называют число, равное
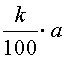
Число a называют базой для вычисления процентов.
ЗАМЕЧАНИЕ. Понятие «проценты» всегда подразумевает существование числа (базы), от которого проценты вычисляются. Проценты не существуют сами по себе.
ПРИМЕР 1. Найти 1% от числа 72 .
РЕШЕНИЕ. 1% от числа 72 вычисляется по формуле
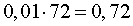
ОТВЕТ. 0,72
ПРИМЕР 2. Найти 5% от числа 48 .
РЕШЕНИЕ. 5% от числа 48 вычисляется по формуле
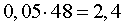
ОТВЕТ 2,4
ПРИМЕР 3. Сколько процентов составляет число 81 от числа 90 ?
РЕШЕНИЕ 1. Предположим, что число 81 составляет x % от числа 90 , и запишем это в следующем виде:
90 ↔ 100%
81 ↔ x %
Для того, чтобы найти неизвестный член пропорции
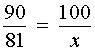
воспользуемся основным свойством пропорции
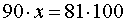
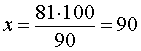
ОТВЕТ. 90%
РЕШЕНИЕ 2. Предположим, что число 81 равно x % от числа 90 , и, в соответствии с определением процентов, составим уравнение
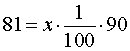
Решая это уравнение, получаем
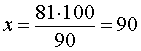
ОТВЕТ 90%
ПРИМЕР 4. Сколько процентов составляет число 320 от числа 50 ?
РЕШЕНИЕ 1. Предположим, что число 320 составляет x % от числа 50 , и запишем это в следующем виде:
50 ↔ 100%
320 ↔ x %
Для того, чтобы найти неизвестный член пропорции
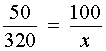
воспользуемся основным свойством пропорции
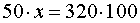
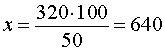
ОТВЕТ. 640%
РЕШЕНИЕ 2. Предположим, что число 320 равно x % от числа 50 , и, в соответствии с определением процентов, составим уравнение
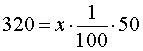
Решая это уравнение, получаем
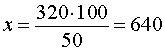 .
.
ОТВЕТ. 640%
ПРИМЕР 5. Найти число, если 30% процентов этого числа равны 18 .
РЕШЕНИЕ. Обозначим искомое число буквой x и, в соответствии с определением процентов, составим уравнение
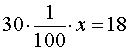
Решая это уравнение, получаем
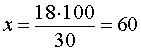
ОТВЕТ. 60
ПРИМЕР 6. Найти число, если 12% процентов этого числа равны 36 .
РЕШЕНИЕ. Обозначим искомое число буквой x и, в соответствии с определением процентов, составим уравнение
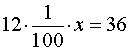
Решая это уравнение, получаем
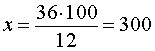
ОТВЕТ. 300
ПРИМЕР 7. Число увеличилось в 2,7 раза. На сколько процентов увеличилось это число?
РЕШЕНИЕ. Обозначим рассматриваемое число буквой a . При увеличении этого числа в 2,7 раза (т.е. при умножении на 2,7) число a увеличивается на число, равное
2,7a – a = 1,7a .
Записывая данные для составления пропорции в виде
a ↔ 100%
1,7a ↔ x %
получаем:
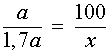
Далее с помощью основного свойства пропорции находим
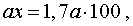
x = 170 .
ОТВЕТ. 170%
ПРИМЕР 8. Число уменьшилось в 2,5 раза. На сколько процентов уменьшилось это число?
РЕШЕНИЕ. Обозначим рассматриваемое число буквой a . При уменьшении этого числа в 2,5 раза (т.е. при делении на 2,5 ) число a уменьшается на число, равное
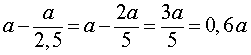
Записывая данные для составления пропорции в виде
a ↔ 100%
0,6a ↔ x %
получаем:
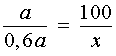
Далее с помощью основного свойства пропорции находим
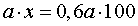
x = 60 .
ОТВЕТ. 60%
ПРИМЕР 9. Число увеличилось на 7% . Во сколько раз увеличилось это число?
РЕШЕНИЕ. Обозначая рассматриваемое число буквой a , а буквой b – число a , увеличенное на 7% , получаем
b = a + 0,07a =1,07a .
Следовательно,
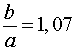 .
.
ОТВЕТ. В 1,07 раза.
ПРИМЕР 10. Число d на 16% меньше числа c . Какую часть составляет число d от числа c ?
РЕШЕНИЕ. Поскольку
d = c – 0,16c =0,84c .
то
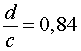
ОТВЕТ. Число d составляет 0,84 от числа c .
ПРИМЕР 11. Налог на добавленную стоимость (НДС) равняется 18% цены товара. Найти цену товара без учета НДС, если товар с учетом НДС стоит 1652 рубля.
РЕШЕНИЕ. Обозначим цену товара без учета НДС буквой a . Стоимость товара с учетом НДС равна
100% + 18% = 118%
от числа a . Следовательно,
1,18a = 1652 ,
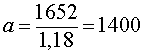
ОТВЕТ. 1400 рублей.
ПРИМЕР 12. Свежие фрукты содержат 82% воды, а сухофрукты содержат 20% воды. Сколько килограммов сухофруктов получится из 1000 килограммов свежих фруктов?
РЕШЕНИЕ. Как свежие фрукты, так и сухофрукты, состоят из сухого вещества и воды, причем при высушивании фруктов вода частично испаряется (ее масса уменьшается), а масса сухого вещества остается неизменной.
| Свежие фрукты | ||
| Вода | Сухое вещество | |
|
Сухофрукты |
||
| Вода | Сухое вещество | |
Поскольку свежие фрукты содержат 82% воды, то масса сухого вещества в них составляет 18% . Поэтому в 1000 килограммов свежих фруктов сухого вещества содержится
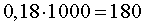 (кг).
(кг).
В сухофруктах вода составляет 20% , а сухое вещество – 80% . Обозначив буквой x массу сухофруктов, полученных из 1000 килограммов свежих фруктов, запишем имеющиеся данные в следующем виде:
x ↔ 100%
180 ↔ 80%
Для того, чтобы найти неизвестный член пропорции
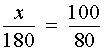
воспользуемся основным свойством пропорции
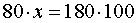
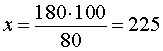
ОТВЕТ. 225кг.
ПРИМЕР 13. Свежие грибы содержат 85% воды, а сухие грибы содержат 10% воды. Из какого количества свежих грибов получится 4,5 килограмма сухих грибов?
РЕШЕНИЕ. Как свежие, так и сухие грибы, состоят из сухого вещества и воды, причем при высушивании свежих грибов вода частично испаряется (ее масса уменьшается), а масса сухого вещества остается неизменной.
| Свежие грибы | ||
| Вода | Сухое вещество | |
|
Сухие грибы |
||
| Сухое вещество | ||
Поскольку сухие грибы содержат 10% воды, то масса сухого вещества в них составляет 90% . Поэтому в 4,5 килограммах сухих грибов сухого вещества содержится
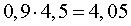 (кг).
(кг).
В свежих грибах вода составляет 85% , а сухое вещество – 15% . Обозначив буквой x массу свежих грибов, необходимых для получения 4,5 килограммов сухих грибов, запишем имеющиеся данные в следующем виде:
x ↔ 100%
4,05 ↔ 15%
Для того, чтобы найти неизвестный член пропорции
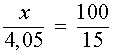
воспользуемся основным свойством пропорции
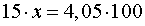
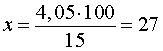
ОТВЕТ. 27кг.
ПРИМЕР 14. На сколько процентов изменится площадь прямоугольника, если его длину увеличить на 20% , а ширину уменьшить на 10% ?
РЕШЕНИЕ. Если обозначить буквой a длину прямоугольника, а буквой b – его ширину, то площадь прямоугольника будет вычисляться по формуле
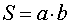
После увеличения длины прямоугольника на 20% его длина станет равной 1,2a . После уменьшения ширины прямоугольника на 10% его ширина станет равной 0,9a . Таким образом, площадь нового прямоугольника станет равной
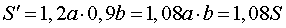
Следовательно, S' составляет 108% от S .
ОТВЕТ. Площадь прямоугольника увеличится на 8% .
Близкие по тематике разделы сайта
Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть раздел нашего справочника «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на смеси, сплавы и растворы, представлены в разделе нашего справочника «Задачи на выполнение работ».
Методы решения задач на смеси, сплавы и растворы, представлены в разделе нашего справочника «Задачи на смеси, сплавы и растворы».
С примерами решения задач на движение можно ознакомиться в разделе нашего справочника «Задачи на движение».
