Справочник по математике Арифметика
Арифметика Проценты
Проценты
Простые и сложные проценты. Предоставление кредитов на основе процентной ставки
Содержание
 |
Кредитное соглашение. Процентные деньги |
 |
Годовая процентная ставка |
 |
Схема простых процентов |
 |
Схема сложных процентов |
 |
Изменяющиеся (плавающие) процентные ставки |
 |
Примеры решения задач |
 |
Темп инфляции |
Кредитное соглашение. Процентные деньги
С того момента, как на Земле появились деньги, появились и люди, которые стали давать их в долг, извлекая из этого прибыль.
ОПРЕДЕЛЕНИЕ 1. Лицо, дающее деньги в долг, называют кредитором. Лицо, берущее деньги в долг, называют заёмщиком.
Предоставление денег в долг происходит в соответствии с кредитным соглашением и осуществляется в различных формах: выдача ссуды, продажа товара в кредит, помещение денег на депозитный счет, получение векселя, приобретение облигаций и т.д.
При заключении кредитного соглашения кредитор и заемщик договариваются о размере кредита, времени и способе его погашения, а также об уровне вознаграждения кредитора.
ОПРЕДЕЛЕНИЕ 2. Плату за предоставление денег в долг, т.е. разницу между деньгами, возвращаемыми заемщиком кредитору, и деньгами, данными кредитором заемщику в долг, называют процентными деньгами.
Будем использовать следующие обозначения:
Z – сумма денег, данных кредитором заемщику в долг,
K – сумма денег, возвращаемая заемщиком кредитору,
D – процентные деньги.
| K = Z + D . | (1) |
Будем рассматривать лишь такие кредитные соглашения, когда долг вместе с процентными деньгами (сумма K ) возвращается заемщиком кредитору одним платежом в конце срока, установленного кредитным соглашением.
Годовая процентная ставка
ОПРЕДЕЛЕНИЕ 3. Годовой процентной ставкой называют отношение процентных денег к деньгам, данным кредитором заемщику в долг, при предоставлении ссуды сроком на 1 год.
Будем обозначать буквами P и p годовую процентную ставку, выраженную в процентах и долях соответственно.
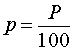 ,
,
причем по определению годовой процентной ставки
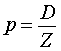 |
(2) |
СЛЕДСТВИЕ 1. Если известны значения p и Z , то, переписывая формулу (2) в виде
D = pZ ,
и, воспользовавшись формулой (1), получаем соотношение для вычисления суммы K :
K = Z + D = Z + pZ ,
из которого следует, что при предоставлении ссуды на срок в 1 год
| K = Z (1 + p) . | (3) |
СЛЕДСТВИЕ 2. Если известны значения p и K , то из формулы (3) можно найти сумму Z :
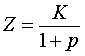 |
(4) |
Схема простых процентов
Будем рассматривать случай, когда срок t возврата долга выражается в годах, например,
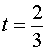 (года) , t = 2 (года), t = 3,4 (года), ...
(года) , t = 2 (года), t = 3,4 (года), ...
Нашей целью является описание двух способов расчета сумм K, возвращаемых заемщиком кредитору (расчеты по схемам простых и сложных процентов на основе процентной ставки).
Отметим особо, что значения p и Z нам известны, а мы вычисляем суммы K.
ОПРЕДЕЛЕНИЕ 4. Расчет по схеме простых процентов на основе годовой процентной ставки заключается в том, что кредитор за каждый год предоставленного кредита получает одни и те же процентные деньги, которые составляют P процентов от суммы долга Z, выплаченной заемщику.
Рассмотрим сначала случай, когда кредит с расчетом по схеме простых процентов предоставляется на целое число лет, и обозначим символами K1 , K2 , ... , Kn суммы, возвращаемые заемщиком кредитору (с учетом процентных денег) за пользование кредитом в течение t = 1, 2, ... , n лет соответственно.
В силу определения 4
K1 = Z + pZ ,
K2 = Z + 2pZ = K1 + pZ ,
...
Kn = Z + npZ = Kn – 1 + pZ ,
откуда вытекает
СЛЕДСТВИЕ 3. Суммы K1 , K2 , ... , Kn , возвращаемые заемщиком кредитору (с учетом процентных денег) за пользование кредитом по схеме простых процентов на основе годовой процентной ставки в течение t = 1, 2, ... , n лет, определяются по формуле
| Km = Z (1 + mp) , m = 1, 2, ... , n | (5) |
и составляют арифметическую прогрессию с первым членом Z (1 + p) и разностью pZ .
Перейдем теперь к рассмотрению случая, когда кредит с расчетом по схеме простых процентов на основе годовой процентной ставки предоставляется на произвольное (не обязательно целое) число лет t (в годах), и, обобщая соотношение (5), сформулируем следующее
УТВЕРЖДЕНИЕ 1. Если кредитное соглашение предусматривает расчет по схеме простых процентов на основе годовой процентной ставки, то по прошествии t лет кредитор получает от заемщика сумму
| K (t) = Z (1 + pt) , | (6) |
а процентные деньги вычисляются по формуле
D (t) = Z (1 + pt) – Z = Zpt .
ЗАМЕЧАНИЕ 1. При t = n , т.е. в случае, когда кредит предоставляется на целое число лет, расчеты по формулам (5) и (6) совпадают.
Схема сложных процентов
ОПРЕДЕЛЕНИЕ 5. Расчет по схеме сложных процентов на основе годовой процентной ставки заключается в том, что кредитор за каждый год предоставленного кредита получает процентные деньги, которые составляют P процентов от всей накопленной к началу этого года суммы долга (с учетом процентных денег).
Поступая по аналогии с простыми процентами, рассмотрим сначала случай, когда кредит с расчетом по схеме сложных процентов предоставляется на целое число лет, и обозначим символами K1 , K2 , ... , Kn суммы, возвращаемые заемщиком кредитору за пользование кредитом в течение t = 1, 2, ... , n лет соответственно.
В силу определения 5
K1 = Z (1 + p) ,
K2 = Z (1 + p)2 = K1 (1 + p) ,
...
Kn = Z (1 + p)n = Kn – 1 (1 + p) ,
откуда вытекает
СЛЕДСТВИЕ 4. Суммы K1 , K2 , ... , Kn , возвращаемые заемщиком кредитору (с учетом процентных денег) за пользование кредитом по схеме сложных процентов с годовой процентной ставкой в течение t = 1, 2, ... , n лет, определяются соотношением
| Km = Z (1 + p)m , m = 1, 2, ... , n | (7) |
и составляют геометрическую прогрессию с первым членом Z (1 + p) и знаменателем (1 + p) .
Перейдем теперь к рассмотрению случая, когда кредит с расчетом по схеме сложных процентов на основе годовой процентной ставки предоставляется на произвольное (не обязательно целое) число лет t (в годах), и, обобщая соотношение (7), сформулируем следующее
УТВЕРЖДЕНИЕ 2. Если кредитное соглашение предусматривает расчет по схеме сложных процентов на основе годовой процентной ставки, то, по прошествии t лет, кредитор получает от заемщика сумму
| K (t) = Z (1 + p)t , | (8) |
а процентные деньги вычисляются по формуле
D (t) = Z (1 + p)t – Z .
Изменяющиеся (плавающие) процентные ставки
В следующих двух примерах кредит (ссуда) предоставляется на основе изменяющихся (плавающих) процентных ставок.
ПРИМЕР 1. Заемщик получил ссуду в 1000000 рублей, которую должен погасить одним платежом через 0,75 года. Расчет производится по схеме простых процентов, причем первые 0,25 года годовая процентная ставка равна 12% , а в оставшееся время годовая процентная ставка равна 16% . Найти сумму, возвращаемую кредитору, и процентные деньги.
РЕШЕНИЕ. Поскольку при расчетах по схеме простых процентов на основе процентной ставки процентные деньги начисляются на сумму долга Z по формуле (6) , то
K (t) = Z (1 + p1t1 + p2t2) ,
где
p1 = 0,12 ; t1 = 0,25 ;
p2 = 0,16 ; t2 = 0,5 .
Таким образом,
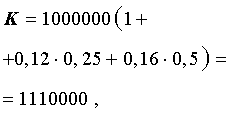 ,
,
D = K – Z = 1100000 – 1000000 = 100000 .
ОТВЕТ. Заемщик возвращает кредитору 1100000 рублей, процентные деньги равны 100000 рублей.
ПРИМЕР 2. Заемщик получил ссуду в 1000000 рублей, которую должен погасить одним платежом через 5 лет. Расчет производится по схеме сложных процентов, причем первые 2 года годовая процентная ставка равна 12% , а в оставшееся время годовая процентная ставка равна 16% . Найти сумму, возвращаемую кредитору, и процентные деньги.
РЕШЕНИЕ. Поскольку при расчетах по схеме сложных процентов на основе процентной ставки процентные деньги за каждый год начисляются на всю накопленную к этому моменту сумму долга по формуле (8), то
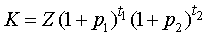 ,
,
где
p1 = 0,12 ; t1 = 2 ;
p2 = 0,16 ; t2 = 3 .
Таким образом
K = 1000000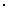 (1 + 0,12)2 (1 + 0,16)3 = 1957987,94 ;
(1 + 0,12)2 (1 + 0,16)3 = 1957987,94 ;
D = K – Z = 1957987,94 – 1000000 = 957987,94 .
ОТВЕТ. Заемщик возвращает кредитору 1957987,94 рублей, процентные деньги равны 957987,94 рублей.
Примеры решения задач
ЗАДАЧА 1. Предприниматель обратился в банк с просьбой о предоставлении ссуды в размере 1000000 рублей сроком на 1 год. Банк выделил ему эту ссуду с годовой процентной ставкой в 20% , при условии погашения ссуды одним платежом в конце срока. Какую сумму должен через год возвратить предприниматель банку? Какие процентные деньги получит банк?
РЕШЕНИЕ. В задаче известны значения Z и p , а найти нужно K и D . Поскольку
Z = 1000000 ; p = 0,2 ;
а предприниматель возвращает банку сумму K , равную
Z + 20% от Z ,
то есть
120% от Z ,
то
K = 1,2Z =1200000 ,
D = 200000 .
ОТВЕТ. Предприниматель возвращает банку 1200000 рублей, процентные деньги банка равняются 200000 рублей.
ЗАДАЧА 2. По истечении первого месяца цена товара увеличилась на 30% , а по истечении следующего месяца цена товара уменьшилась на 10% . На сколько процентов изменилась первоначальная цена товара за 2 месяца?
РЕШЕНИЕ. Обозначим первоначальную цену товара буквой a . По истечении первого месяца цена товара стала равной 1,3 a . По условию задачи за второй месяц новая цена товара (база для вычисления процентов), равная 1,3 a , уменьшилась на 10% и стала равной
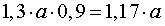 ,
,
ОТВЕТ. Первоначальная цена товара за 2 месяца увеличилась на 17% .
ЗАДАЧА 3. Цена товара увеличилась на 25% . На сколько процентов нужно снизить цену товара, чтобы она стала первоначальной?
РЕШЕНИЕ. Обозначим первоначальную цену товара буквой c . После увеличения на 25% новая цена товара стала равной 1,25 c . Следовательно, для того, чтобы вернуться к первоначальному уровню c , новая цена товара (база для вычисления процентов), должна уменьшиться на сумму 0,25 c . Таким образом, мы должны определить, сколько процентов составляет число 0,25c от числа 1,25c :
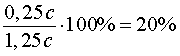
ОТВЕТ. Цену товара нужно снизить на 20% .
ЗАДАЧА 4. Банковский вклад, нетронутый в течение года, в конце этого года увеличивается на 10% . На сколько процентов увеличится вклад, нетронутый в течение трех лет?
РЕШЕНИЕ. Обозначим первоначальную сумму вклада буквой Z и проведем расчет по схеме сложных процентов. Используя формулу (8), находим
K (3) = Z (1 + 0,1)3 = 1,331 Z
Таким образом, денежная сумма Z , нетронутая в течение трех лет, увеличивается на сумму 0,331 Z ; то есть на 33,1% .
ОТВЕТ. Вклад увеличится на 33,1% .
Темп инфляции
ОПРЕДЕЛЕНИЕ 8. Месячным темпом инфляции называют такое количество процентов, на которое возрастают цены товаров за месяц, по сравнению с предыдущим месяцем.
ЗАДАЧА 5. Месячный темп инфляции равен 5% . На сколько процентов возрастают цены за год?
РЕШЕНИЕ. Инфляция является процессом, развивающимся по схеме сложных процентов. Если обозначить цену товара в первый день года буквой Z , то, используя формулу (8), находим цену товара через 12 месяцев:
K (12) = Z (1 + 0,05)12 = 1,7959 Z
Следовательно, с начала года цена товара Z увеличилась на сумму 0,7959 Z ; т.е. увеличилась на 79,59% .
ОТВЕТ. Цены вырастают за год на 79,59% .
ЗАМЕЧАНИЕ 2. Если бы мы для решения этой задачи вместо формулы (8) применили формулу (6), которая относится к расчету по схеме простых процентов, что является серьёзной ошибкой, то мы бы получили неверный ответ, свидетельствующий о том, что при месячном темпе инфляции в 5% цены за год вырастают на 60% .
Близкие по тематике разделы сайта
Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть раздел нашего справочника «Проценты. Решение задач на проценты», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ, представлены в разделе нашего справочника «Задачи на выполнение работ».
Методы решения задач на смеси, сплавы и растворы, представлены в разделе нашего справочника «Задачи на смеси, сплавы и растворы».
С методами, используемыми при решении задач на движение, можно ознакомиться в разделе нашего справочника «Задачи на движение».
