Справочник по математике
Арифметика Обыкновенные и десятичные дроби
Арифметические действия с дробями, выраженными в различных формах
Содержание
 |
Обращение простой дроби в десятичную дробь |
|
Арифметические действия с дробями, выраженными в различных формах |
Обращение простой дроби в десятичную дробь
Если знаменатель несократимой простой дроби или несократимого смешанного нецелого числа содержит в качестве простых множителей лишь числа 2 и 5, то при обращении в десятичную дробь получается конечная десятичная дробь.
Если же знаменатель несократимой простой дроби или несократимого смешанного числа содержит при разложении на простые множители хотя бы один из простых множителей, отличный от чисел 2 и 5, то при обращении в десятичную дробь получается бесконечная периодическая десятичная дробь.
Например,
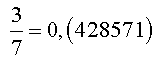
Арифметические действия с дробями, выраженными в различных формах
Для того, чтобы избежать ошибок при выполнении арифметических действий над числами, имеющими вид простых дробей, десятичных дробей или смешанных чисел, рекомендуется сначала обратить все числа в единую форму, а затем выполнить все необходимые арифметические действия. После этого, если требуется, результат можно обратить в нужную форму.
В качестве примера решим задачу № 1.024 из "Сборника задач по математике для поступающих в ВУЗы" (Под редакцией М.И. Сканави).
ЗАДАЧА. Выполнить действия:
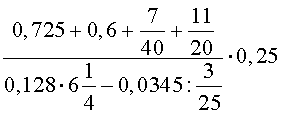
РЕШЕНИЕ. Выполним сначала действия в числителе дроби:
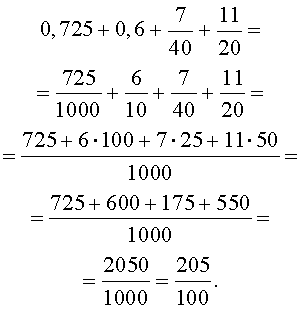
Теперь выполним действия в знаменателе дроби:
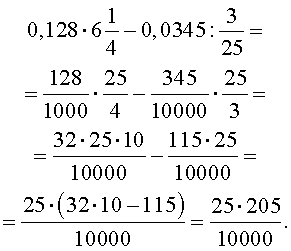
Далее получаем:
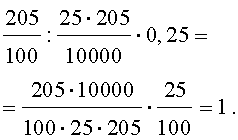
ОТВЕТ: 1.