Справочник по математике
Арифметика Рациональные и иррациональные числа
Понятие о вещественных (действительных) числах, рациональные и иррациональные числа
Содержание
 |
Рациональные и иррациональные числа. Понятие о вещественных числах |
|
Иррациональность числа  |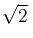
|
Десятичные приближения иррациональных чисел с недостатком и с избытком |
Рациональные и иррациональные числа. Понятие о вещественных числах
Целые числа и рациональные дроби (простые дроби и смешанные числа) составляют множество рациональных чисел, которое принято обозначать буквой Q .
Каждое из рациональных чисел можно представить в виде
,
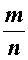где m – целое число, а n – натуральное число.
При обращении рациональных дробей в десятичные дроби получаются конечные и бесконечные периодические десятичные дроби.
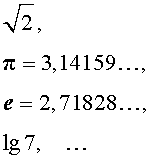
и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Множество вещественных чисел обозначают буквой R .
Иррациональность числа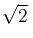
Проведем доказательство иррациональности числа 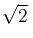методом «от противного». С этой целью предположим, что число 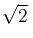является рациональным числом. Тогда существует дробь вида
,
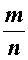удовлетворяющая равенству
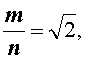
и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:
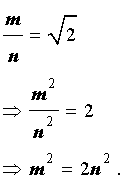
Отсюда вытекает, что число m2 является четным числом, а, значит, и число m является четным числом. Действительно, если мы предположим противное, т.е. предположим, что число m является нечетным числом, то найдется такое целое число k , которое удовлетворяет соотношению
m = 2k + 1 .
Следовательно,
m2 = (2k + 1)2 =
=4k2 + 4k +1 ,
т.е. m является нечетным числом. Полученное противоречие доказывает, что число m является четным числом. Значит, найдется такое целое число k , которое удовлетворяет соотношению
m = 2k .
Поэтому,
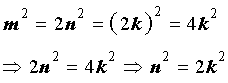
Отсюда вытекает, что число n2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби
.
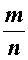Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению
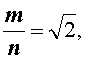
не существует. Следовательно, число 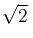является иррациональным числом, что и требовалось доказать.
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число
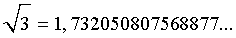
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа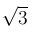 
с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа 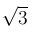отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.
Если последний десятичный знак каждого десятичного приближения числа с недостатком увеличить на 1 , то получится десятичное приближение числа с избытком.
Само число 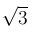располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.
Для числа 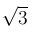возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:
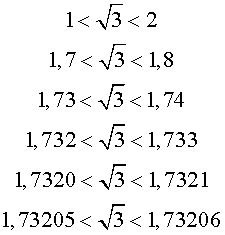
и т.д.
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.