Справочник по математикеГеометрия (Планиметрия) Площади

Вывод формулы Герона и формулы Брахмагупты

Содержание

	Вывод формулы Герона
	Вывод формулы Брахмагупты

Вывод формулы Герона

УТВЕРЖДЕНИЕ 1 (формула Герона). Площадь произвольного треугольника можно найти по формуле Герона:

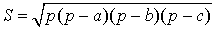
где   a , b , c   – длины сторон треугольника, а   p   – полупериметр треугольника, т.е.

.

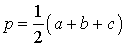ДОКАЗАТЕЛЬСТВО.

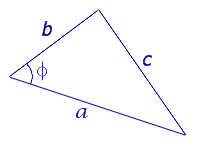
Рис.1

Поскольку (рис.1)

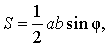
то

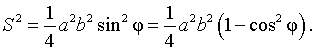
Воспользовавшись теоремой косинусов, получаем:

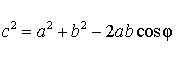
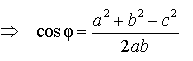
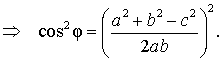
Следовательно,

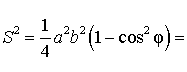
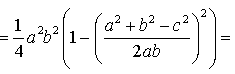
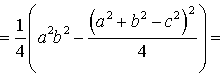
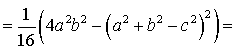
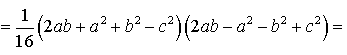
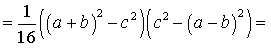
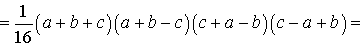
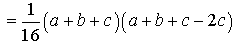
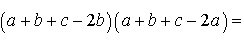
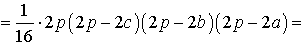
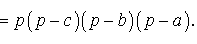
Таким образом,

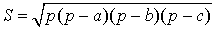
что и требовалось доказать.

Вывод формулы Брахмагупты

УТВЕРЖДЕНИЕ 2 (формула Брахмагупты). Площадь четырёхугольника, вписанного в окружность, можно найти по формуле Брахмагупты:

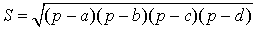
где   a , b , c , d   – длины сторон четырёхугольника, а   p   – полупериметр, т.е.

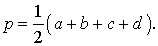
ДОКАЗАТЕЛЬСТВО.

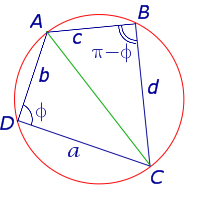
Рис.2

Если угол   D   четырёхугольника   ABCD   обозначить буквой   φ   (рис.2), то, поскольку сумма противоположных углов вписанного четырёхугольника равна   π ,   угол   B   будет равен   π – φ .   По этой причине

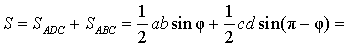
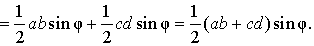
Следовательно,

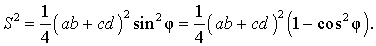
Применяя теорему косинусов к треугольнику   ACD ,   получаем:

AC ² = a² + b² – 2bc cos φ .

Применяя теорему косинусов к треугольнику   ABC ,   получаем:

AC ² = c² + d ² – 2cd cos (π – φ) =

=c² + d ² + 2cd cos φ .

Следовательно,

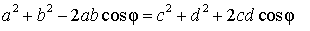
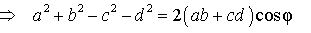
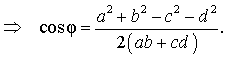
Поэтому

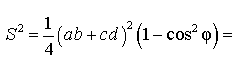
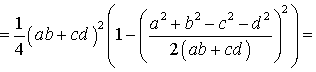
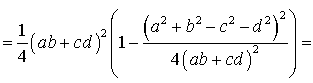
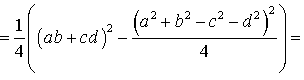
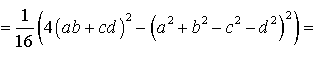
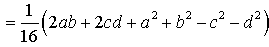
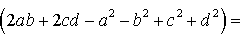
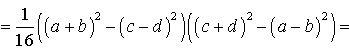
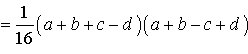
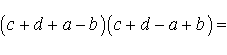
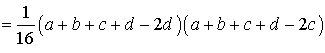
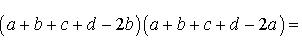
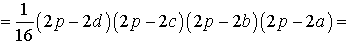
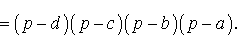
Буквой   p   здесь обозначен полупериметр четырехугольника   ABCD

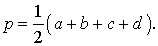
Формула Брахмагупты доказана.