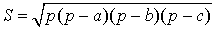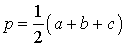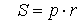Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Площади
Площади
Площадь треугольника
Содержание

Формулы для площади треугольника
Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.
| Произвольный треугольник |
|
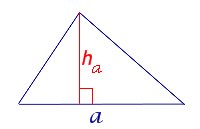
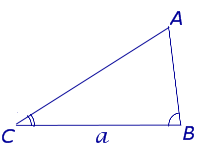
Формула для площади треугольника через сторону и опущенную на нее высоту
a – любая сторона треугольника, ha – высота, опущенная на эту сторону |
|
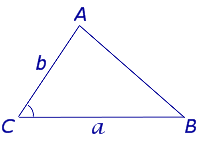
Формула для площади треугольника через две стороны и угол между ними
a и b – две любые стороны треугольника, С – угол между ними |
|
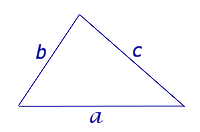
Формула Герона
a, b, c – стороны треугольника, p – полупериметр
|
|
Формула для площади треугольника через сторону и два прилежащих к ней угла
a – любая сторона, B, С – прилежащие к ней углы |
|
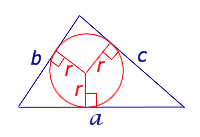
Формула для площади треугольника через стороны треугольника и радиус вписанной окружности
a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр
|
|
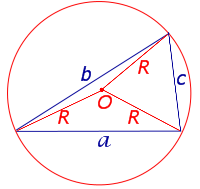
Формула для площади треугольника через стороны треугольника и радиус описанной окружности
a, b, c – стороны, R – радиус описанной окружности |
|
Формула для площади треугольника через углы треугольника и радиус описанной окружности
A, B, С – углы, R – радиус описанной окружности |
| Равносторонний (правильный) треугольник |
|
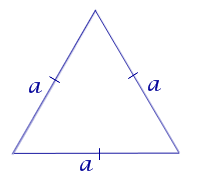
Формула для площади равностороннего (правильного) треугольника через его сторону
a – сторона |
|
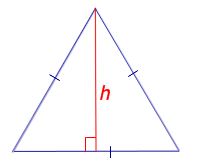
Формула для площади равностороннего (правильного) треугольника через его высоту
h – высота |
|
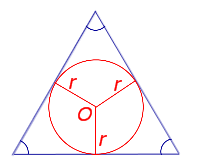
Формула для площади равностороннего (правильного) треугольника через радиус вписанной окружности
r – радиус вписанной окружности |
|
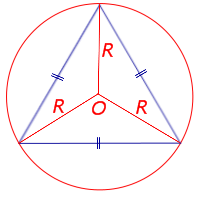
Формула для площади равностороннего (правильного) треугольника через радиус описанной окружности
R – радиус описанной окружности |
| Прямоугольный треугольник |
|
Формула для площади прямоугольного треугольника через катеты
a и b – катеты |
|
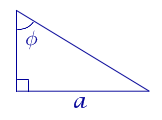
Формула для площади прямоугольного треугольника через катет и прилежащий острый угол
a – катет, φ – прилежащий острый угол |
|
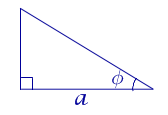
Формула для площади прямоугольного треугольника через катет и противолежащий острый угол
a – катет, φ – противолежащий острый угол |
|
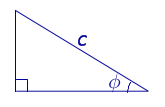
Формула для площади прямоугольного треугольника через гипотенузу и острый угол
c – гипотенуза, φ – любой из острых углов |
Вывод формул для площади произвольного треугольника
УТВЕРЖДЕНИЕ 1. Площадь треугольника можно найти по формуле
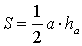
где a – любая сторона треугольника, а ha – высота, опущенная на эту сторону.
ДОКАЗАТЕЛЬСТВО.
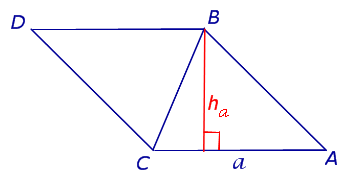
Рис. 1
Достроив треугольник ABC до параллелограмма ABDC (рис. 1), получим
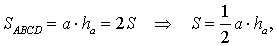
что и требовалось доказать.
УТВЕРЖДЕНИЕ 2. Площадь треугольника можно найти по формуле
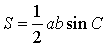
где a и b – две любые стороны треугольника, а С – угол между ними.
ДОКАЗАТЕЛЬСТВО.
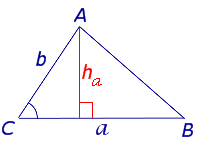
Рис. 2
Поскольку
ha = b sin C ,
то, в силу утверждения 1, справедлива формула
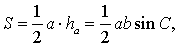
что и требовалось доказать.
УТВЕРЖДЕНИЕ 3. Площадь треугольника можно найти по формуле
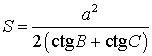
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.
ЗАМЕЧАНИЕ. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.
ДОКАЗАТЕЛЬСТВО.
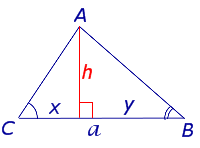
Рис. 3
Поскольку (рис.3)
x = hactg C , y = hactg B ,
то
a = x + y = hactg C + hactg B = ha( ctg C + ctg B) .
Следовательно,
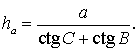
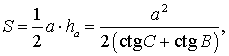
что и требовалось доказать.
УТВЕРЖДЕНИЕ 4. Площадь треугольника можно найти по формуле
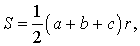
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.
ДОКАЗАТЕЛЬСТВО.
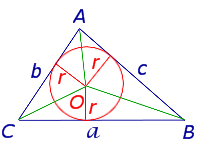
Рис. 4
Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим
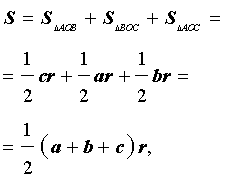
что и требовалось доказать.
УТВЕРЖДЕНИЕ 5. Площадь треугольника можно найти по формуле
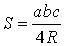
где a, b, c – стороны треугольника, а R – радиус описанной окружности.
ДОКАЗАТЕЛЬСТВО.
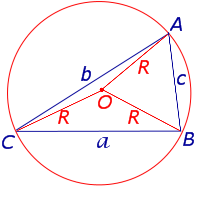
Рис. 5
В силу теоремы синусов справедливо равенство
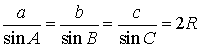 .
.
Следовательно,
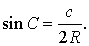
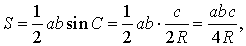
что и требовалось доказать.
УТВЕРЖДЕНИЕ 6. Площадь треугольника можно найти по формуле:
S = 2R2 sin A sin B sin C ,
где A, B, С – углы треугольника, а R – радиус описанной окружности.
ДОКАЗАТЕЛЬСТВО.
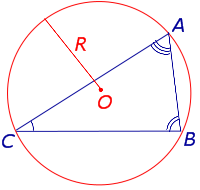
Рис. 6
В силу теоремы синусов справедливо равенство
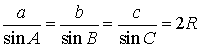 .
.
Поэтому
a = 2R sin A , b = 2R sin B , c = 2R sin C ,
В силу утверждения 5
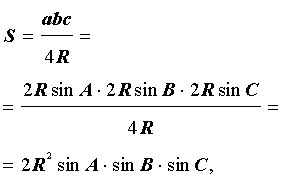
что и требовалось доказать.
Вывод формул для площади равностороннего треугольника
УТВЕРЖДЕНИЕ 7.
-
Если a – сторона равностороннего треугольника, то его площадь
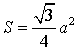
-
Если h – высота равностороннего треугольника, то его площадь
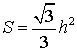
-
Если r – радиус вписанной в равносторонний треугольник окружности, то его площадь
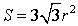
-
Если R – радиус описанной около равностороннего треугольника окружности, то его площадь
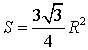
ДОКАЗАТЕЛЬСТВО.
-
Рассмотрим рисунок 7.
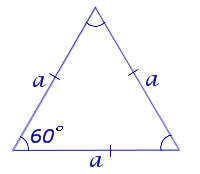
Рис. 7
В силу утверждения 2
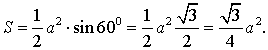
-
Рассмотрим рисунок 8.
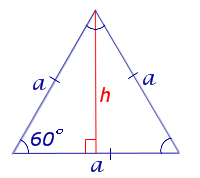
Рис. 8
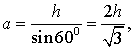
то, в силу утверждения 1, справедлива формула
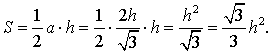
-
Рассмотрим рисунок 9.
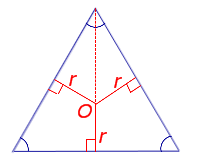
Рис. 9
Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство
h = 3r.
Следовательно,
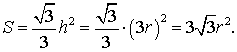
-
Рассмотрим рисунок 10.
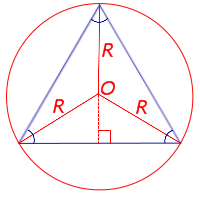
Рис. 10
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство
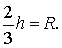
Следовательно,
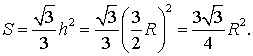
Доказательство утверждения 7 завершено.
Вывод формул для площади прямоугольного треугольника
УТВЕРЖДЕНИЕ 8.
-
Если a и b – катеты прямоугольного треугольника, то его площадь
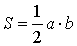
-
Если a – катет прямоугольного треугольника, а φ – прилежащий к этому катету острый угол, то площадь прямоугольного треугольника
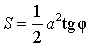
-
Если a – катет прямоугольного треугольника, а φ – противолежащий этому катету острый угол, то площадь прямоугольного треугольника
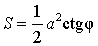
-
Если c – гипотенуза прямоугольного треугольника, а φ – острый угол, то площадь прямоугольного треугольника
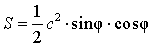
ДОКАЗАТЕЛЬСТВО.
-
Рассмотрим рисунок 11.
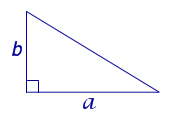
Рис. 11
В силу утверждения 2
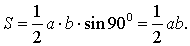
-
Рассмотрим рисунок 12.
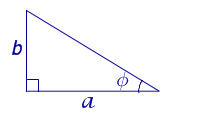
Рис. 12
b = a tg φ ,
то
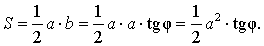
-
Рассмотрим рисунок 13.
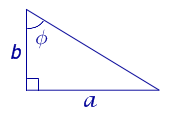
Рис. 13
b = a ctg φ ,
то
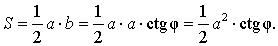
-
Рассмотрим рисунок 14.
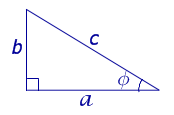
Рис. 14
a = c cos φ , b = c sin φ ,
то
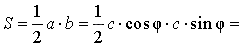
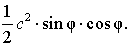
Доказательство утверждения 8 завершено.