Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Высота треугольника. Задача Фаньяно
Содержание

Высота треугольника. Свойство высоты прямоугольного треугольника
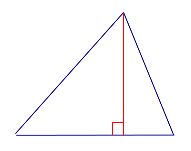
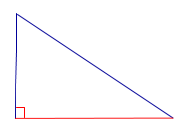
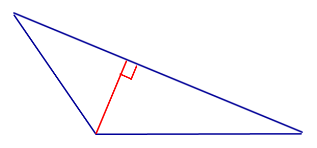
ОПРЕДЕЛЕНИЕ 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
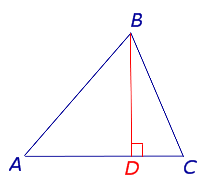
Рис.1
На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
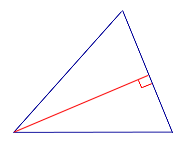
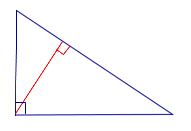
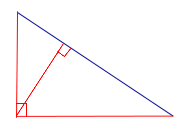
УТВЕРЖДЕНИЕ. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
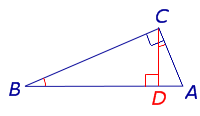
Рис.2
ДОКАЗАТЕЛЬСТВО. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
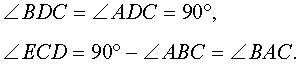
В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,
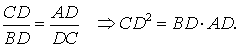
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.
Расположение высот у треугольников различных типов
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
| Остроугольный треугольник |
|
Все высоты остроугольного треугольника лежат внутри треугольника. |
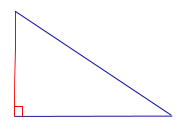
| Прямоугольный треугольник |
|
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
| Тупоугольный треугольник |
|
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
Ортоцентр треугольника
ТЕОРЕМА 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.
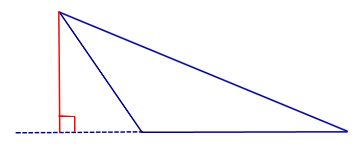
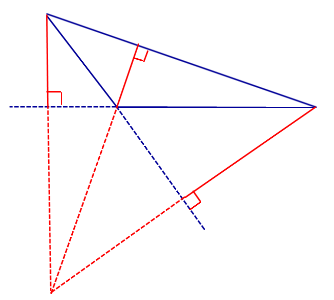
ДОКАЗАТЕЛЬСТВО. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
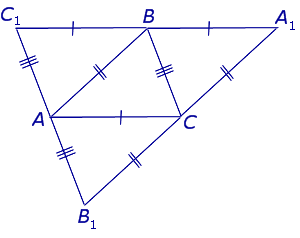
Рис.3
Обозначим точки пересечения этих прямых символами A1, B1 и C1, как показано на рисунке 3.
В силу параллельности прямых AC и C1A1, а также BC и C1B1 четырёхугольники AC1BC и ABA1C – параллелограммы, откуда вытекают равенства
C1B = AC = BA1.
Следовательно, точка B является серединой стороны C1A1.
В силу параллельности прямых BC и C1B1, а также AB и B1A1 четырёхугольники AC1BC и ABCB1 – параллелограммы, откуда вытекают равенства
C1A = BC = A1B1.
Следовательно, точка A является серединой стороны C1B1.
В силу параллельности прямых AB и B1A1, а также AC и C1A1 четырёхугольники ABA1C и ABCB1 – параллелограммы, откуда вытекают равенства
A1C = AB = B1C.
Следовательно, точка C является серединой стороны B1A1.
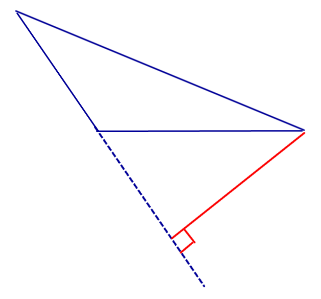
Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A1B1C1 (рис. 4),
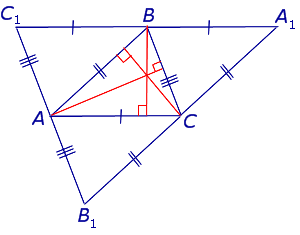
Рис.4
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
ОПРЕДЕЛЕНИЕ 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
Расположение ортоцентров у треугольников различных типов
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
| Остроугольный треугольник |
|
Ортоцентр остроугольного треугольника лежит внутри треугольника. |
| Прямоугольный треугольник |
|
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла |
| Тупоугольный треугольник |
|
Ортоцентр тупоугольного треугольника лежит вне треугольника. В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника. |
Ортоцентрический треугольник
Решим следующую задачу.
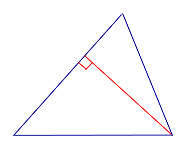
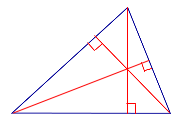
ЗАДАЧА. В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC.
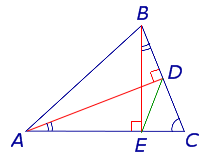
Рис.5
РЕШЕНИЕ. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
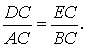
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
Из подобия треугольников ABC и EDC (рис.5) вытекает важное следствие.
СЛЕДСТВИЕ 1.
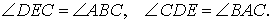
ОПРЕДЕЛЕНИЕ 3. Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
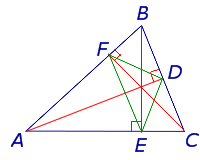
Рис.6
Из определения 3 и следствия 1 вытекает следствие 2.
СЛЕДСТВИЕ 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
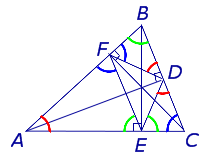
Рис.7
Тогда справедливы равенства
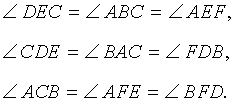
Из следствия 2 вытекает теорема 2.
ТЕОРЕМА 2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
ДОКАЗАТЕЛЬСТВО. Воспользовавшись следствием 2, получаем:
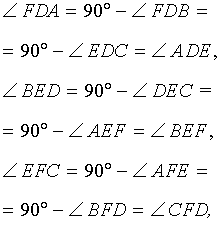
что и требовалось доказать.
Задача Фаньяно
ЗАДАЧА ФАНЬЯНО. Рассматриваются всевозможные треугольники DEF, вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC.
РЕШЕНИЕ. Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC, и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
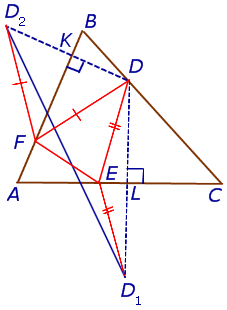
Рис.8
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
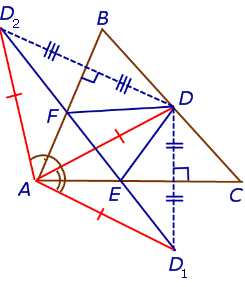
Рис.9
Заметим также, что выполнено равенство
AD = AD1 = AD2.
Кроме того, выполнено равенство
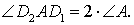
Поэтому
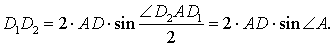
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
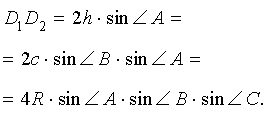
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
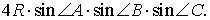
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
ЛЕММА. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
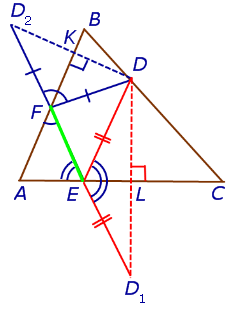
Рис.10
В этом случае отрезок D1D2 проходит через точки F и E.
ДОКАЗАТЕЛЬСТВО. Заметим, что в силу следствия 2 выполняются равенства:
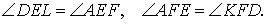
Кроме того, в силу равенства треугольников DFK и KFD2, а также в силу равенства треугольников DEL и LED1 выполняются равенства:
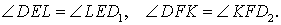
Следовательно,
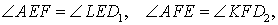
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1, F, E, D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.