Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Свойства и признаки равнобедренного треугольника
| Определение равнобедренного треугольника |
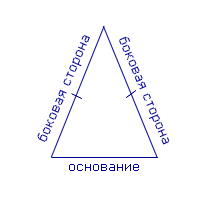
Определение Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство углов при основании равнобедренного треугольника |
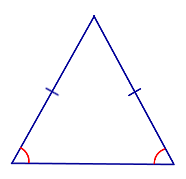
Свойство Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треугольника: два равных угла треугольника |

Признак Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
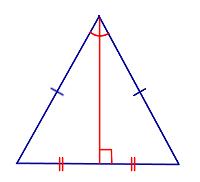
Свойство В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
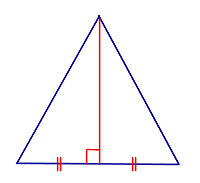
Признак Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
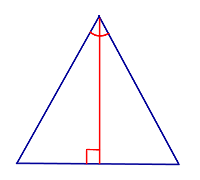
Признак Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
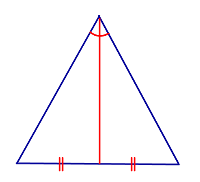
Признак Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
