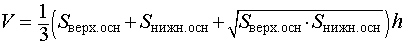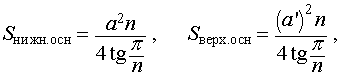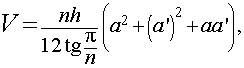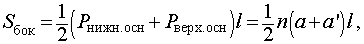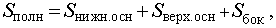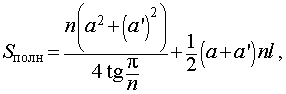учебные материалы

Справочник по математикеусеченная пирамида вершины ребра грани апофема высота площадь боковой полной поверхности объем усеченной пирамиды правильная усеченная пирамида теорема ЭйлераГеометрия (Стереометрия)усеченная пирамида вершины ребра грани апофема высота площадь боковой полной поверхности объем усеченной пирамиды правильная усеченная пирамида теорема Эйлера Пирамиды

 

Усеченные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды

Содержание

усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера Усеченные пирамиды. Теорема Эйлера для усеченных пирамид
правильная усеченная пирамида апофема Правильные усеченные пирамиды
площадь боковой поверхности усеченной пирамиды площадь полной поверхности для усеченной пирамиды объем усеченной пирамиды Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды
 

усеченная пирамида вершины ребра грани апофема высота площадь боковой полной поверхности объем усеченной пирамиды правильная усеченная пирамида теорема Эйлера

Усеченные пирамиды. Теорема Эйлера для усеченных пирамид

ОПРЕДЕЛЕНИЯ

усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания высота боковая поверхность полная поверхность теорема Эйлера апофема

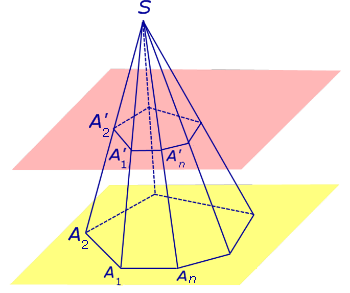
Плоскость, параллельная основанию пирамиды   SA1A2 ... An   и пересекающая все боковые ребра пирамиды в точках   A'1 , A'2 , ... , A'n ,   делит пирамиду   SA1A2 ... An   на две части: пирамиду   SA'1A'2 ... A'n   и усеченную пирамиду   A1A2 ... AnA'1A'2 ... A'n   (рис. 1).

усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды

Рис.1

усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Рис.2
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Многоугольник   A1A2 ... An   называют нижним основанием усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Многоугольник   A'1A'2 ... A'n   называют верхним основанием усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Расстояние между плоскостями оснований усеченной пирамиды называют высотой усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Точки   A1 , A2 , ... , An , A'1 , A'2 , ... , A'n   называют вершинами оснований усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Отрезки   A1A'1 , A2A'2 , ... , AnA'n   называют боковыми ребрами усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Стороны многоугольников   A1A2 ... An ,   A'1A'2 ... A'n   называют ребрами оснований усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Трапеции   A1A'1A'2A2 ,   A2A'2A'3A3 ,   ... ,   AnA'nA'1A1   называют боковыми гранями усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Множество всех боковых граней усеченной пирамиды составляет боковую поверхность усеченной пирамиды.
усеченная пирамида вершины усеченной пирамиды боковые ребра усеченной пирамиды ребра оснований усеченной пирамиды боковые грани усеченной пирамиды основания усеченной пирамиды высота усеченной пирамиды боковая поверхность усеченной пирамиды полная поверхность пирамиды теорема Эйлера

Полная поверхность усеченной пирамиды состоит из оснований усеченной пирамиды и ее боковой поверхности.

ТЕОРЕМА ЭЙЛЕРА . Для любой усеченной пирамиды справедливо равенство:

число
вершин
+
число
граней
–
число
ребер
= 2

ДОКАЗАТЕЛЬСТВО. Заметим, что у n - угольной усеченной пирамиды   2n   вершин,   n   боковых граней,   2   основания,   2n   ребер оснований и   n   боковых ребер. Следовательно, у n - угольной усеченной пирамиды   (n + 2)   грани и   3n   ребер.

Поскольку

2n + (n + 2) – 3n = 2

то теорема Эйлера доказана.

Правильные усеченные пирамиды

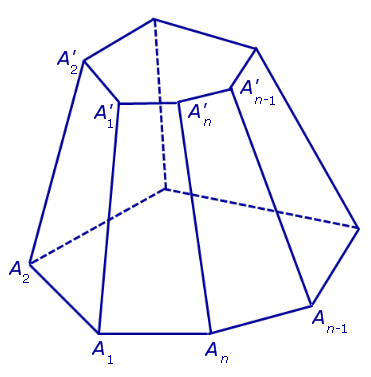
Плоскость, параллельная основанию правильной пирамиды   SA1A2 ... An   и пересекающая все боковые ребра пирамиды в точках   A'1 , A'2 , ... , A'n , делит пирамиду   SA1A2 ... An   на две части: правильную пирамиду   SA'1A'2 ... A'n   и правильную усеченную пирамиду   A1A2 ... AnA'1A'2 ... A'n   (рис. 3).

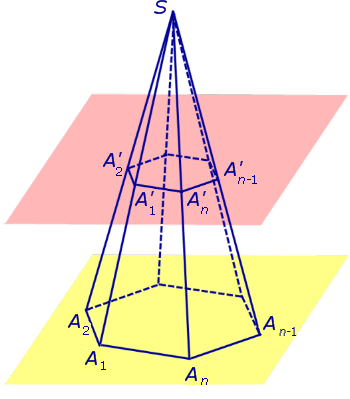
правильная усеченная пирамида апофема

Рис.3

ОПРЕДЕЛЕНИЕ 2. Высоту боковой грани правильной усеченной пирамиды называют апофемой правильной усеченной пирамиды (рис 4).

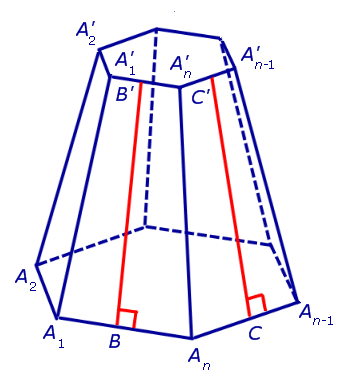
правильная усеченная пирамида апофема

Рис.4

На рис. 4 отрезок   B'B   – апофема грани   A1A'1A'nAn   и отрезок   C'C   – апофема грани   AnA'nA'n - 1An - 1

СВОЙСТВА ПРАВИЛЬНОЙ УСЕЧЕННОЙ ПИРАМИДЫ:

правильная усеченная пирамида апофема

Все боковые ребра правильной усеченной пирамиды равны.
правильная усеченная пирамида апофема

Все боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями.
правильная усеченная пирамида апофема

У любой правильной усеченной пирамиды все апофемы равны.
правильная усеченная пирамида апофема

Все боковые ребра правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные углы.
правильная усеченная пирамида апофема

Все боковые ребра правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные углы.
правильная усеченная пирамида апофема

Все боковые грани правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные двугранные углы.
правильная усеченная пирамида апофема

Все боковые грани правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные двугранные углы.
правильная усеченная пирамида апофема

Отрезок, соединяющий центры верхнего и нижнего оснований правильной усеченной пирамиды, перпендикулярен плоскостям оснований правильной усеченной пирамиды. Длина этого отрезка равна высоте правильной усеченной пирамиды.

Формулы для объема, площади боковой и полной поверхности усеченной пирамиды

Введем следующие обозначения

V объем усеченной пирамиды
Sбок площадь боковой поверхности усеченной пирамиды
Sполн площадь полной поверхности усеченной пирамиды
Sверх.осн площадь верхнего основания усеченной пирамиды
Sнижн.осн площадь нижнего основания усеченной пирамиды
Pверх.осн периметр верхнего основания усеченной пирамиды
Pнижн.осн периметр нижнего основания усеченной пирамиды

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности усеченной пирамиды:

Произвольная усеченная пирамида

объем усеченной пирамиды

Формулы для объема, площади боковой и полной поверхности:

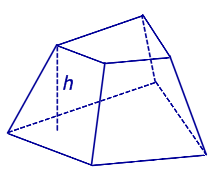
объем усеченной пирамиды

где h – высота усеченной пирамиды.
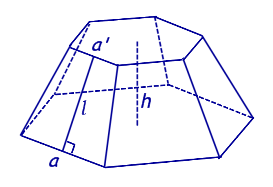
Правильная n – угольная усеченная пирамида

объем правильной усеченной пирамиды площадь боковой поверхности правильной усеченной пирамиды площадь полной поверхности правильной усеченной пирамиды

Формулы для объема, площади боковой и полной поверхности:

формула площади правильного n-угольника

(см. раздел «правильные многоугольники»),

объем усеченной пирамиды

* * *

объем усеченной пирамиды

* * *

площадь боковой поверхности правильной усеченной пирамиды

* * *

площадь полной поверхности правильной усеченной пирамиды

площадь полной поверхности правильной усеченной пирамиды

где
h  – высота правильной усеченной пирамиды,
a – длина ребра нижнего основания правильной пирамиды,
a' – длина ребра верхнего основания правильной пирамиды,
l – длина апофемы правильной усеченной пирамиды.

Справочник по математике для школьников

Геометрия (стереометрия)

Учебные пособия для школьников

Демоверсии ЕГЭ

© «Резольвента - учебные материалы», 2009-2024 

Rambler's Top100  Рейтинг@Mail.ru

Метрика Яндекса
 Яндекс.Метрика