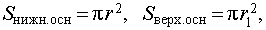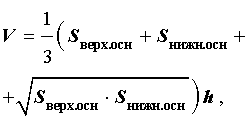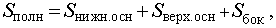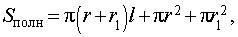Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Конусы
Конусы
Конусы. Усеченные конусы. Объем, площади боковой и полной поверхностей конуса и усеченного конуса
Содержание
 |
Конусы |
 |
Усеченные конусы |
 |
Объем, площади боковой и полной поверхностей конуса и усеченного конуса |

Конусы
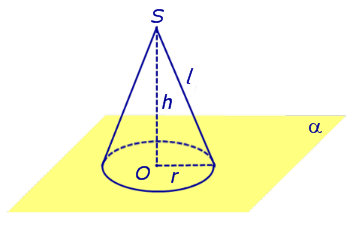
Рассмотрим произвольную плоскость α, точку S, не лежащую на плоскости α, и перпендикуляр SO, опущенный из точки S на плоскость α (точка O – основание перпендикуляра). Рассмотрим также произвольный круг с центром в точке O, лежащий на плоскости α.
ОПРЕДЕЛЕНИЯ
 |
Конусом называют фигуру, состоящую из всех отрезков, соединяющих точку S с точками указанного круга с центром в точке O, лежащего на плоскости α (рис. 1).
Рис.1 |
 |
Точку S называют вершиной конуса. |
 |
Отрезок SO называют осью конуса. |
 |
Расстояние от точки S до плоскости α (длину отрезка SO) называют высотой конуса. |
 |
Круг с центром в точке O, лежащий на плоскости α, называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость α называют плоскостью основания конуса. |
 |
Отрезки, соединяющие точку S с точками окружности называют образующими конуса. |
 |
Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность). |
 |
Полная поверхность конуса состоит из основания конуса и его боковой поверхности. |
ЗАМЕЧАНИЕ 1. Отрезок SO часто называют высотой конуса.
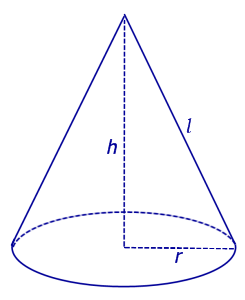
ЗАМЕЧАНИЕ 2. Все образующие конуса имеют одинаковую длину. У конуса с высотой h и радиусом основания r длина образующих равна
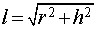
Усеченные конусы
Рассмотрим конус с вершиной S, осью SO, радиусом основания r и высотой h. Плоскость β, параллельная плоскости основания конуса и расположенная на расстоянии h1 от вершины S, пересекает конус по кругу радиуса r1 с центром в точке O1 (рис. 2).
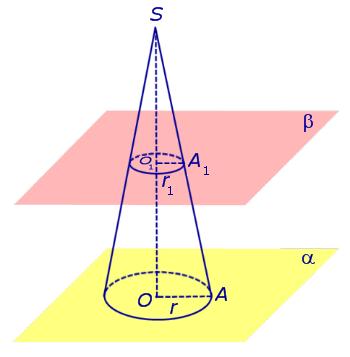
Рис.2
Из подобия прямоугольных треугольников SOA и SO1A1 можно выразить радиус r1 через известные величины r, h и h1:
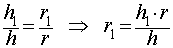
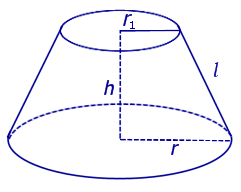
Таким образом, плоскость β делит конус на две части: конус с осью SO1 и радиусом основания r1, а также вторую часть, называемую усеченным конусом (рис. 3).
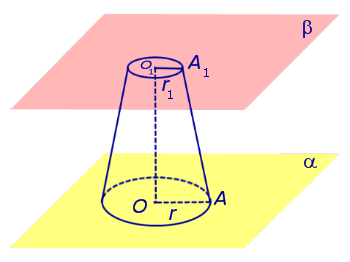
Рис.3
Усеченный конус ограничен двумя основаниями: кругом с центром в точке O радиуса r на плоскости α и кругом с центром в точке O1 радиуса r1 на плоскости β, а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями α и β. Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями α и β, называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок AA1.
Высотой усеченного конуса называют расстояние между плоскостями оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна h – h1.
Объем, площади боковой и полной поверхностей конуса и усеченного конуса
Введем следующие обозначения:
| V | объем конуса (объем усеченного конуса) |
| Sбок | площадь боковой поверхности конуса (площадь боковой поверхности усеченного конуса) |
| Sполн | площадь полной поверхности конуса (площадь полной поверхности усеченного конуса) |
| Sосн | площадь основания конуса |
| Sверх.осн | площадь верхнего основания усеченного конуса |
| Sнижн.осн | площадь нижнего основания усеченного конуса |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности конуса, а также формулы для вычисления объема, площади боковой и полной поверхности усеченного конуса.
| Конус |
|
Формулы для объема, площади боковой и полной поверхности: Sосн = πr2,
Sбок= πrl, Sполн = πr2 + πrl, где |
| Усеченный конус |
|
Формулы для объема, площади боковой и полной поверхности:
Sбок= π (r + r1)l ,
где l – длина образующей усеченного конуса. |
ЗАМЕЧАНИЕ 3. Формула для вычисления объема конуса
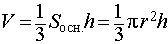
может быть получена из формулы объема правильной n – угольной пирамиды
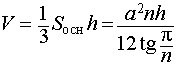
при помощи предельного перехода, когда число сторон правильной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
ЗАМЕЧАНИЕ 4. Формула для вычисления объема усеченного конуса
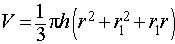
может быть получена из формулы объема правильной усеченной n – угольной пирамиды
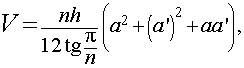
при помощи предельного перехода, когда число сторон правильной усеченной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.