Справочник по математикеГеометрия (Стереометрия) Прямые и плоскости в пространстве

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

ТЕОРЕМА. Пусть   p₁   и   p₂   – две произвольные скрещивающиеся прямые. Если рассмотреть всевозможные прямые   A₁A₂,   такие, что точка   A₁   лежит на прямой   p₁,   а точка   A₂   лежит на прямой   p₂,   то будут выполнены следующие два утверждения:

1. Среди всех прямых   A₁A₂   существует единственная прямая, перпендикулярная к прямой   p₁   и к прямой   p₂   (общий перпендикуляр к двум скрещивающимся прямым).
2. Среди всех отрезков   A₁A₂   наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

ДОКАЗАТЕЛЬСТВО. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

Через произвольную точку прямой   p₁   проведем прямую 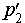, параллельную прямой   p₂ ,   а через произвольную точку прямой   p₂   проведем прямую 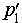, параллельную прямой   p₁ .   Обозначим буквой   α   плоскость, проходящую через прямые   p₁   и 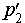, а буквой   β   плоскость, проходящую через прямые   p₂   и 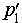(рис 1).

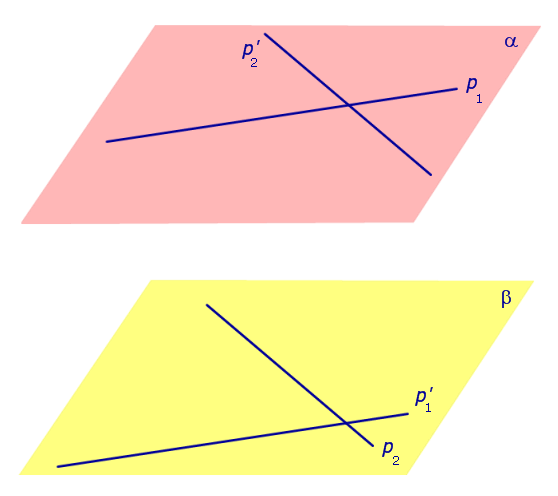
Рис.1

Поскольку прямая   p₁   параллельна прямой 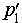, лежащей на плоскости   β ,   то по признаку параллельности прямой и плоскости прямая   p₁   параллельна плоскости   β.   Точно так же, поскольку прямая 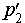параллельна прямой   p₂ ,   лежащей на плоскости   β ,   то прямая 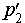по признаку параллельности прямой и плоскости параллельна плоскости   β.   Таким образом, плоскость   α   содержит две пересекающиеся прямые   p₁   и 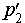, параллельные плоскости   β.   В силу признака параллельности плоскостей заключаем, что плоскости   α   и   β   параллельны.

Спроектируем прямую p₁ на плоскость   β.   Получим прямую 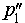, являющуюся проекцией прямой   p₁,   и обозначим точку пересечения прямых   p₂   и 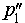буквой   B₂   (рис. 2).

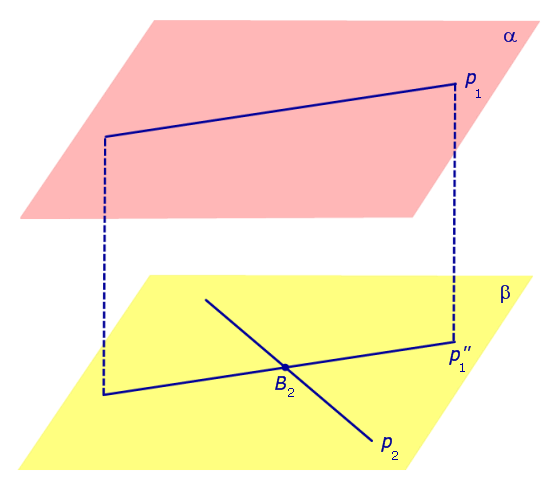
Рис.2

Спроектируем теперь прямую   p₂   на плоскость   α .   Получим прямую 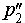, являющуюся проекцией прямой   p₂ ,   и обозначим точку пересечения прямых   p₁   и 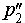буквой   B₁   (рис. 3).

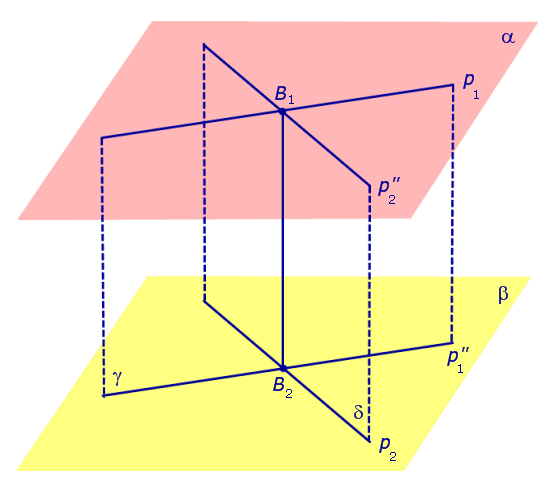
Рис.3

Поскольку точка   B₂   является проекцией точки   B₁ ,   то прямая   B₁B₂   перпендикулярна каждой из плоскостей   α   и   β .   Следовательно, прямая   B₁B₂   перпендикулярна и к каждой из прямых   p₁   и   p₂ .   Таким образом,   B₁B₂   – общий перпендикуляр к скрещивающимся прямым   p₁   и   p₂ .

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

Докажем, что построенная прямая   B₁B₂   является единственным общим перпендикуляром к прямым   p₁   и   p₂ .

Заметим, что любая прямая, перпендикулярная к   p₁   и к   p₂ ,   по признаку перпендикулярности прямой и плоскости будет перпендикулярна к построенным выше плоскостям   α   и   β   (рис. 3). Кроме того, общий перпендикуляр к прямым   p₁   и   p₂   должен проходить через точку, лежащую на прямой   p₁ ,   а значит, этот перпендикуляр должен лежать в плоскости   γ,   перпендикулярной к плоскостям   α   и   β,   и проходящей через прямую   p₁ .

С другой стороны общий перпендикуляр к прямым   p₁   и   p₂   должен проходить через точку, лежащую на прямой   p₂ ,   а значит, этот перпендикуляр должен лежать в плоскости   δ,   перпендикулярной к плоскостям   α   и   β,   и проходящей через прямую   p₂ .

Таким образом, общий перпендикуляр к прямым   p₁   и   p₂   является линией пересечения плоскостей   γ   и   δ,   то есть прямой   B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок   A₁A₂ , у которого конец   A₁   лежит на плоскости   α , а конец   A₂   лежит на плоскости   β . Опустим перпендикуляр из точки   A₁   на плоскость   β   и обозначим основание этого перпендикуляра символом   A₃   (рис. 4).

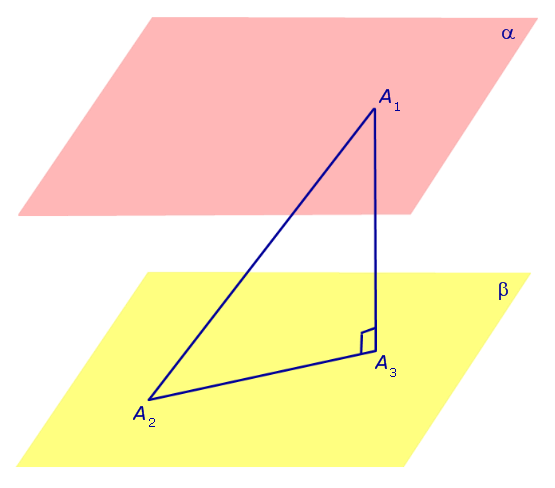
Рис.4

      Если отрезок   A₁A₂   не является перпендикуляром к плоскостям   α   и   β,   то точка   A₃   не совпадет с точкой   A₂,   и треугольник   A₁A₂A₃   будет прямоугольным треугольником с гипотенузой   A₁A₂   и катетом   A₁A₃.   Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

A₁A₃ < A₁A₂ .

Поскольку длина отрезка   A₁A₃ , как и длина отрезка   B₁B₂ ,   равна расстоянию между параллельными плоскостями α и β , то утверждение 2 доказано.

ЗАМЕЧАНИЕ. Длину отрезка   B₁B₂,   лежащего на общем перпендикуляре к двум скрещивающимся прямым, и называют расстоянием между скрещивающимися прямыми.