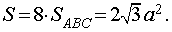Справочник по математикеГеометрия (Стереометрия) Октаэдры

Октаэдр. Объем и площадь поверхности октаэдра

Содержание

	Октаэдр
	Объем и площадь поверхности октаэдра

Октаэдр. Теорема Эйлера для октаэдра

Рассмотрим куб и обозначим символами   A   и   A',   B   и   B',   C   и   C'   центры его противоположных граней (рис. 1).

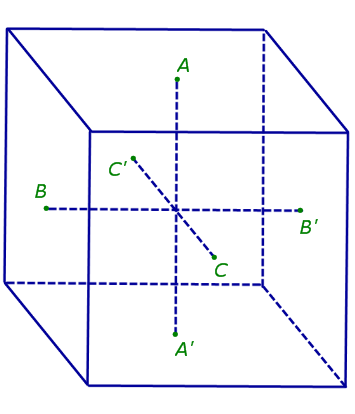
Рис.1

Фигуру, состоящую из двух равных правильных четырехугольных пирамид   ABC'B'C   и   A'BC'B'C   с общим основанием   BC'B'C, называют октаэдром (рис. 2).

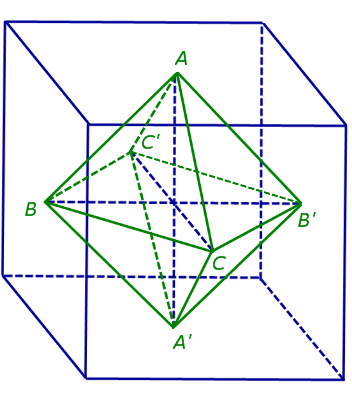
Рис.2

Вершины правильных четырехугольных пирамид   ABC'B'C   и   A'BC'B'C   называют вершинами октаэдра, ребра этих пирамид называют ребрами октаэдра, а боковые грани пирамид называют гранями октаэдра. Отрезки   AA',   BB'   и   CC' называют диагоналями октаэдра.

ТЕОРЕМА ЭЙЛЕРА. Для октаэдра справедливо равенство:

Для доказательства теоремы Эйлера достаточно заметить, что у октаэдра   8   граней,   6   вершин и  12   ребер.

СВОЙСТВА ОКТАЭДРА:

	Все ребра октаэдра равны.
	Все грани октаэдра являются равными равносторонними (правильными) треугольниками.
	Диагонали октаэдра равны.
	Диагонали октаэдра взаимно перпендикулярны.
	Диагонали октаэдра пересекаются в одной точке и делятся в точке пересечения пополам.

Объем и площадь поверхности октаэдра

Обозначим буквой   a   длину ребра октаэдра   AA'BB'CC' (рис. 3).

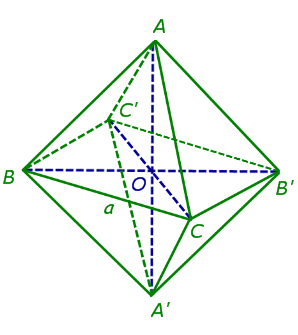
Рис.3

Для того, чтобы найти объем октаэдра   AA'BB'CC',   заметим, что этот объем равен удвоенному объему правильной четырехугольной пирамиды   ABC'B'C.   Основанием пирамиды   ABC'B'C   является квадрат со стороной   a,   а высота пирамиды равна длине отрезка   AO.

Следовательно, площадь основания пирамиды

S_BCB'C' = a ²,

высота пирамиды

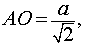
объем пирамиды

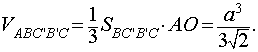
Поэтому объем октаэдра

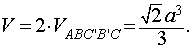
Поскольку площадь грани октаэдра

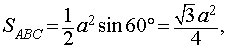
то площадь поверхности октаэдра