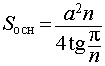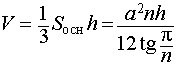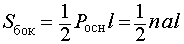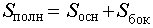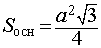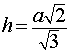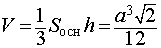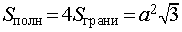Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Пирамиды
Пирамиды
Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
Содержание

Пирамиды. Теорема Эйлера для пирамид
ОПРЕДЕЛЕНИЯ
 |
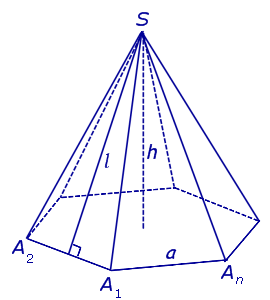
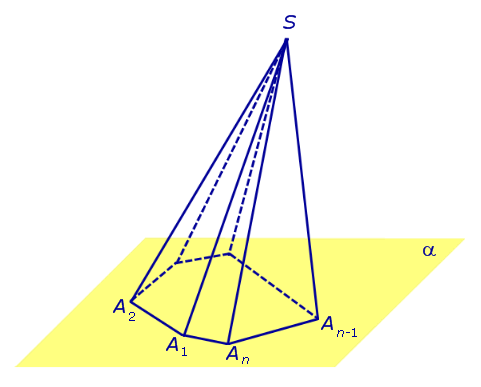
Рассмотрим произвольную плоскость α , произвольный выпуклый n – угольник A1A2 ... An , расположенный в этой плоскости, и точку S , не лежащую в плоскости α . Пирамидой (n - угольной пирамидой) называют фигуру, образованную отрезками, соединяющими точку S со всеми точками многоугольника A1A2 ... An (рис. 1) . ЗАМЕЧАНИЕ 1. Напомним, что многоугольник A1A2 ... An состоит из замкнутой ломаной линии A1A2 ... An и ограниченной ею части плоскости.
Рис.1 |
 |
Точку S называют вершиной пирамиды. |
 |
Многоугольник A1A2 ... An называют основанием пирамиды. |
 |
Точки A1, A2, ... , An называют вершинами основания пирамиды. |
 |
Точки A1 , A2 , ... , An , S часто называют просто вершинами пирамиды. |
 |
Расстояние от точки S до плоскости α называют высотой пирамиды. |
 |
Отрезки SA1 , SA2 , ... , SAn называют боковыми ребрами пирамиды. |
 |
Стороны многоугольника A1A2 ... An называют ребрами основания пирамиды. |
 |
Боковые ребра и ребра основания пирамиды часто называют просто ребрами пирамиды. |
 |
Треугольники SA1A2 , SA2A3 , ... , SAnA1 называют боковыми гранями пирамиды. |
 |
Множество всех боковых граней пирамиды составляет боковую поверхность пирамиды. |
 |
Боковые грани и основание пирамиды часто называют просто гранями пирамиды. |
 |
Полная поверхность пирамиды состоит из основания пирамиды и ее боковой поверхности. |
ТЕОРЕМА ЭЙЛЕРА . Для любой пирамиды справедливо равенство:
|
+ |
|
– |
|
= | 2 |
ДОКАЗАТЕЛЬСТВО. Заметим, что у n - угольной пирамиды (n + 1) вершина, n боковых граней, 1 основание, n ребер основания и n боковых ребер. Следовательно, у n - угольной пирамиды (n + 1) грань и 2n ребер.
Поскольку
(n + 1) + (n + 1) – 2n = 2
то теорема Эйлера доказана.
Правильные пирамиды. Свойства правильной пирамиды
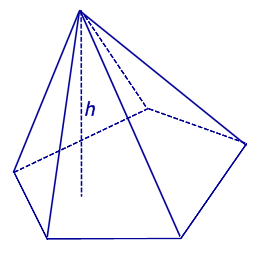
ОПРЕДЕЛЕНИЕ 2. Правильной n - угольной пирамидой (правильной пирамидой) называют такую n - угольную пирамиду, у которой основанием является правильный n - угольник A1A2 ... An , а основанием перпендикуляра, опущенного из точки S на плоскость α , является центр правильного n - угольника A1A2 ... An (рис 2).
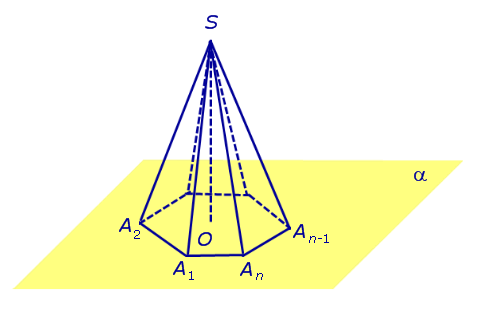
Рис.2
ЗАМЕЧАНИЕ 2. Если центр основания A1A2 ... An правильной пирамиды SA1A2 ... An обозначить буквой O , то длина отрезка SO будет равняться высоте пирамиды. Часто и сам отрезок SO называют высотой пирамиды, опущенной из вершины S .
ОПРЕДЕЛЕНИЕ 3. Высоту боковой грани правильной пирамиды, опущенную из вершины S , называют апофемой.
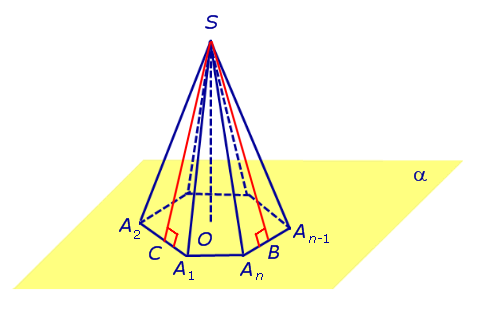
Рис.3
На рисунке 3 отрезок SB – апофема грани SAnAn-1 и отрезок SC – апофема грани SA2A1.
ЗАМЕЧАНИЕ 3 . У любой правильной n – угольной пирамиды можно провести n апофем.
СВОЙСТВА ПРАВИЛЬНОЙ ПИРАМИДЫ:
 |
Все боковые ребра правильной пирамиды равны. |
 |
Все боковые грани правильной пирамиды являются равными равнобедренными треугольниками. |
 |
У любой правильной пирамиды все апофемы равны. |
 |
Все боковые ребра правильной пирамиды образуют с плоскостью основания пирамиды равные углы. |
Тетраэдры. Правильные тетраэдры
ОПРЕДЕЛЕНИЕ 4. Произвольную треугольную пирамиду называют тетраэдром.
УТВЕРЖДЕНИЕ. У любой правильной треугольной пирамиды противоположные ребра попарно перпендикулярны.
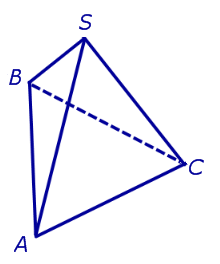
ДОКАЗАТЕЛЬСТВО. Рассмотрим правильную треугольную пирамиду SABC и пару ее противоположных ребер, например, AC и BS. Обозначим буквой D середину ребра AC. Поскольку отрезки BD и SD являются медианами в равнобедренных треугольниках ABC и ASC, то BD и SD перпендикулярны ребру AC (рис. 4).
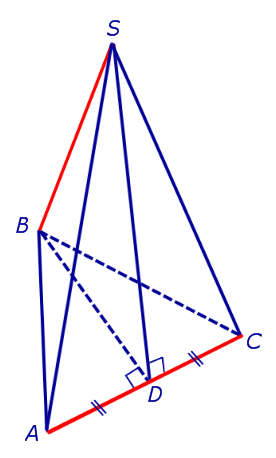
Рис.4
По признаку перпендикулярности прямой и плоскости заключаем, что прямая AC перпендикулярна плоскости BSD. Следовательно, прямая AC перпендикулярна прямой BS, что и требовалось доказать.
ОПРЕДЕЛЕНИЕ 5. Правильную треугольную пирамиду, у которой все ребра равны, называют правильным тетраэдром (рис. 5).
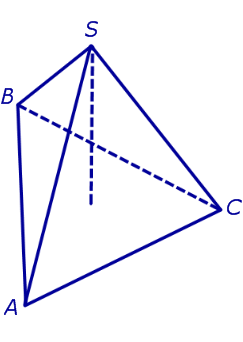
Рис.5
ЗАДАЧА. Найти высоту правильного тетраэдра с ребром a .
РЕШЕНИЕ. Рассмотрим правильный тетраэдр SABC. Пусть точка O – основание перпендикуляра, опущенного из вершины S на плоскость ABC. Поскольку SABC – правильная пирамида, то точка O является точкой пересечения медиан равностороннего треугольника ABC. Следовательно,
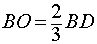
где буквой D обозначена середина ребра AC (рис. 6).
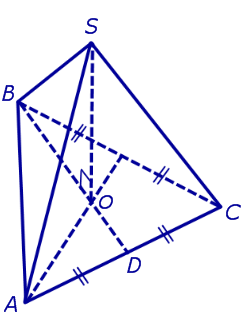
Рис.6
Так как
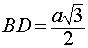 ,
,
то
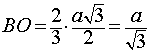 .
.
По теореме Пифагора из треугольника BSO находим
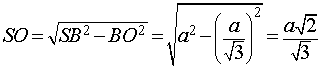
ОТВЕТ. 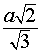
Формулы для объема, площади боковой и полной поверхности пирамиды
Введем следующие обозначения
| V | объем пирамиды |
| Sбок | площадь боковой поверхности пирамиды |
| Sполн | площадь полной поверхности пирамиды |
| Sосн | площадь основания пирамиды |
| Pосн | периметр основания пирамиды |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности пирамиды:
| Произвольная пирамида |
|
Формула для объема:
где h – высота пирамиды. |
| Правильная n – угольная пирамида |
|
Формулы для объема, площади боковой и полной поверхности:
(см. раздел «правильные многоугольники»),
где |
| Правильный тетраэдр |
|
Формулы для объема и площади полной поверхности:
(см. раздел «правильные многоугольники»), Высота правильного тетраэдра равна
где |


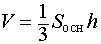 ,
,