Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Прямые и плоскости в пространстве
Прямые и плоскости в пространстве
Ортогональная проекция прямой на плоскость. Угол между прямой и плоскостью. Теорема о трех перпендикулярах
Содержание
 |
Проекция точки на плоскость. Проекция прямой на плоскость |
 |
Угол между прямой и плоскостью |
 |
Теорема о трех перпендикулярах. Обратная теорема |

Проекция прямой на плоскость
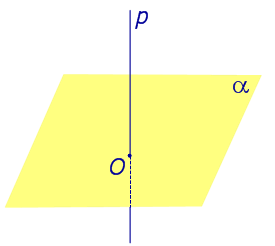
ОПРЕДЕЛЕНИЕ 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
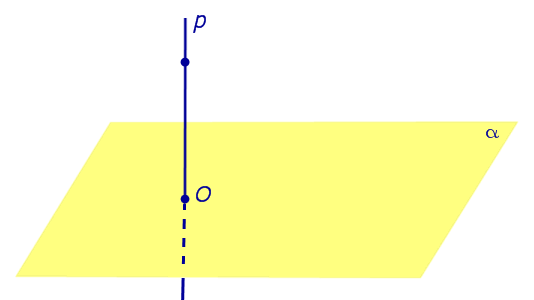
Рис.1
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
ЗАМЕЧАНИЕ 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
ЗАМЕЧАНИЕ 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
ОПРЕДЕЛЕНИЕ 2. Проекцией фигуры a на плоскость α называют фигуру a', образованную проекциями всех точек фигуры a на плоскость α.
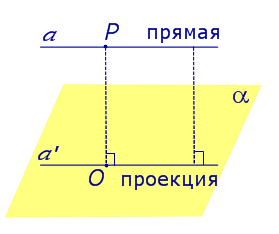
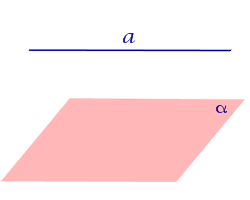
ОПРЕДЕЛЕНИЕ 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
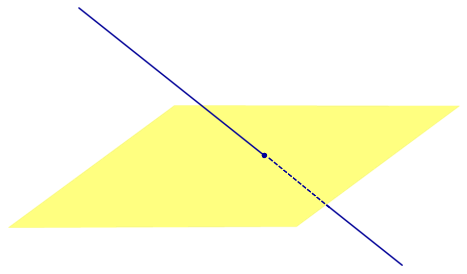
Рис.2
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в таблице
| Свойство проекции наклонной к плоскости на плоскость |
|
Свойство Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P' является проекцией произвольной точки P этой прямой на плоскость α, то прямая P'O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
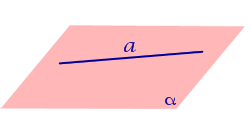
| Свойство проекции прямой, параллельной плоскости, на эту плоскость |
|
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α. Свойство Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a', лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO |
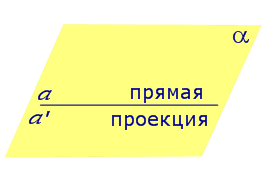
| Свойство проекции прямой, лежащей на плоскости, на эту плоскость |
|
Свойство Если прямая a лежит в плоскости, то ее проекция a', совпадает с прямой a |
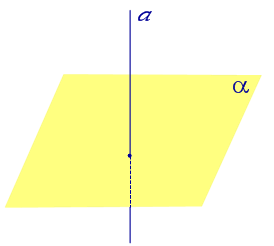
| Свойство проекции прямой, перпендикулярной к плоскости, на эту плоскость |
|
Свойство Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α |
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в таблице.
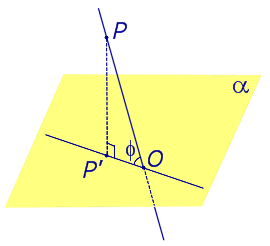
| Определение угла между наклонной к плоскости и плоскостью |
|
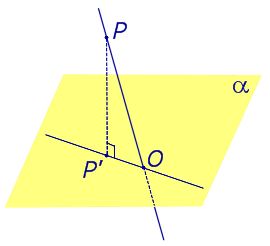
Определение Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P'O ) На рисунке это угол φ. |
| Определение угла между прямой, параллельной плоскости, и плоскостью |
|
Определение Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю |
| Определение угла между прямой, лежащей на плоскости, и плоскостью |
|
Определение Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю |
| Определение угла между прямой, перпендикулярной к плоскости, и плоскостью |
|
Определение Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( |
Теорема о трех перпендикулярах
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a' на плоскость α перпендикулярна к прямой b.
ДОКАЗАТЕЛЬСТВО. Рассмотрим следующий рисунок 3.
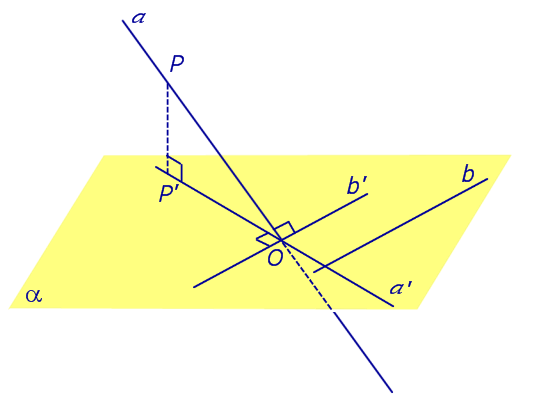
Рис.3
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P' – это проекция точки P на плоскость α. Проведем через точку O прямую b', параллельную прямой b. Если прямая b проходит через точку O, то прямая b', совпадет с прямой b.
Поскольку PP' – перпендикуляр к плоскости α, то прямая PP' перпендикулярна к прямой b'. Прямая a перпендикулярна к прямой b' по условию. Таким образом, прямая b' перпендикулярна к двум пересекающимся прямым PO и PP', лежащим в плоскости POP'. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b' перпендикулярна к плоскости POP', откуда вытекает, что прямая b' перпендикулярна и к прямой a', лежащей на плоскости POP'.
Теорема доказана.
ТЕОРЕМА, ОБРАТНАЯ К ТЕОРЕМЕ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если проекция a' наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
ДОКАЗАТЕЛЬСТВО. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.

Рис.3
Прямая a' перпендикулярна к прямой b по условию обратной теоремы. Прямая PP' перпендикулярна к прямой b', поскольку PP' – перпендикуляр к плоскости α. Таким образом, прямая b', перпендикулярна к двум пересекающимся прямым P'O и PP', лежащим в плоскости POP'. В силу признака перпендикулярности прямой и плоскости прямая b' перпендикулярна к плоскости POP'. Тогда, в частности, прямая b' перпендикулярна к прямой a, лежащей на плоскости POP'.
Теорема доказана.

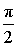 радиан)
радиан)