Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Прямые и плоскости в пространстве
Прямые и плоскости в пространстве
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости. Расстояние от точки до плоскости
Содержание
 |
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости |
 |
Свойства перпендикуляра к плоскости. Расстояние от точки до плоскости |

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости
ОПРЕДЕЛЕНИЕ. Прямой, перпендикулярной к плоскости, называют такую прямую, которая перпендикулярна к каждой прямой, лежащей на этой плоскости.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в некоторой плоскости, то прямая перпендикулярна к этой плоскости.
ДОКАЗАТЕЛЬСТВО. Рассмотрим сначала следующий случай.
Предположим, что прямая p, пересекающая плоскость α в точке O, перпендикулярна к прямым a и b, лежащим на плоскости α и проходящим через точку O. Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c, лежащей на плоскости α и проходящей через точку O.
С этой целью отметим на прямой a произвольную точку A, а на прямой b произвольную точку B (рис. 1).
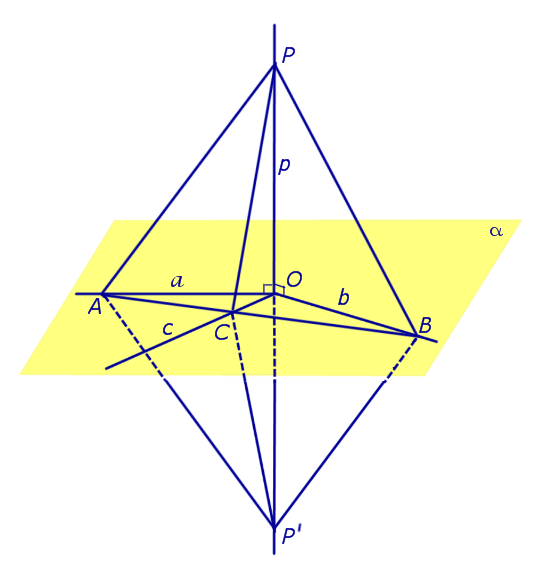
Рис.1
Проведем прямую AB и обозначим буквой C точку пересечения прямых AB и c. Отметим на прямой p произвольную точку P и обозначим символом P' точку, расположенную на прямой p так, чтобы точка O оказалась серединой отрезка PP'. Поскольку прямые OA и OB являются серединными перпендикулярами к отрезку PP', то справедливы равенства
AP = AP', BP = BP'
Из этих равенств, а также поскольку отрезок AB является общей стороной треугольников APB и AP'B, заключаем, что в силу признака равенства треугольников по трем сторонам треугольники APB и AP'B равны. Следовательно,
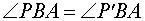
Отсюда в силу признака равенства треугольников по двум сторонам и углу между ними заключаем, что треугольник PBС равен треугольнику P'BС (BP = BP', 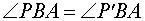 , сторона BС - общая). Следовательно,
, сторона BС - общая). Следовательно,
СP = СP',
откуда вытекает, что точка С лежит на серединном перпендикуляре к отрезку PP'.
Таким образом, прямые PO и c перпендикулярны, что и требовалось доказать в рассматриваемом случае.
Теперь перейдем к общему случаю.
Предположим, что что прямая p, пересекающая плоскость α в точке O, перпендикулярна к прямым a и b, лежащим на плоскости α . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c, лежащей плоскости α (рис. 2).
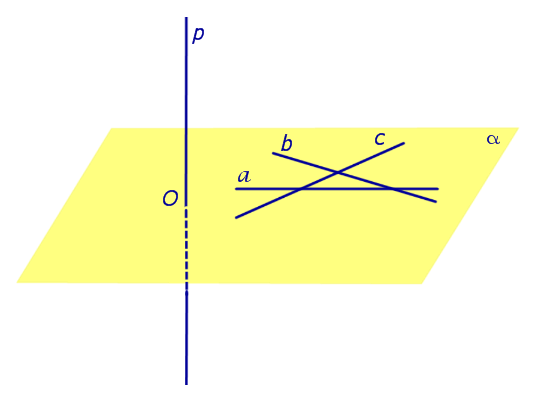
Рис.2
С этой целью проведем через точку O прямые a', b' и c' соответственно параллельные прямым a, b и c .
По определению угла между скрещивающимися прямыми прямая будет перпендикулярна прямым a' и b', проходящим через точку O, и мы оказываемся в условиях уже рассмотренного случая.
Доказательство признака перпендикулярности прямой и плоскости завершено.
ЗАМЕЧАНИЕ. Прямую, перпендикулярную к плоскости, часто называют перпендикуляром к плоскости. Точку пересечения прямой, перпендикулярной к плоскости, с самой плоскостью называют основанием перпендикуляра.
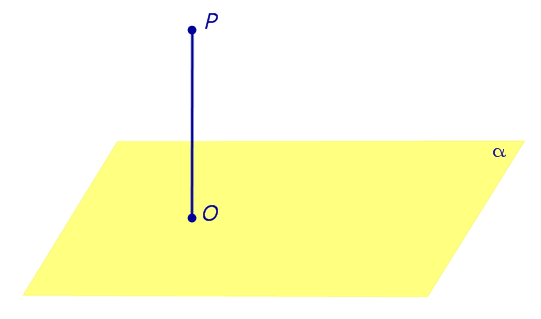
Так, например, на рисунке 1 точка O является основанием перпендикуляра, опущенного из точки P на плоскость α .
Свойства перпендикуляра к плоскости
Перечислим следующие свойства перпендикуляра к плоскости и признака перпендикулярности плоскостей, доказательства которых мы оставляем читателю в качестве полезных упражнений.
| Свойство перпендикуляра к плоскости |
|
Свойство Из любой точки можно опустить перпендикуляр на любую плоскость |
| Определение расстояния от точки до плоскости |
|
Определение Если точка O - основание перпендикуляра, опущенного из точки P на плоскость α, то длину отрезка PO называют расстоянием от точки P до плоскости α. |
| Свойство двух перпендикуляров к плоскости |
|
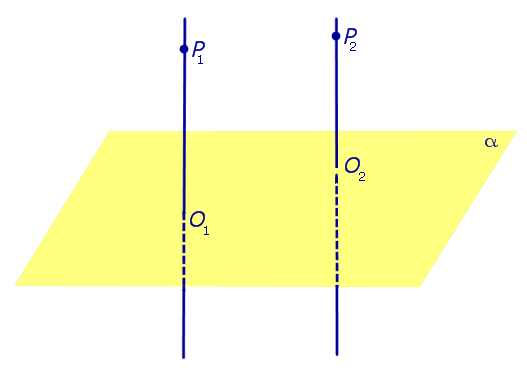
Свойство Два любых перпендикуляра к плоскости параллельны |
| Свойство двух плоскостей, перпендикулярных к одной прямой |
|
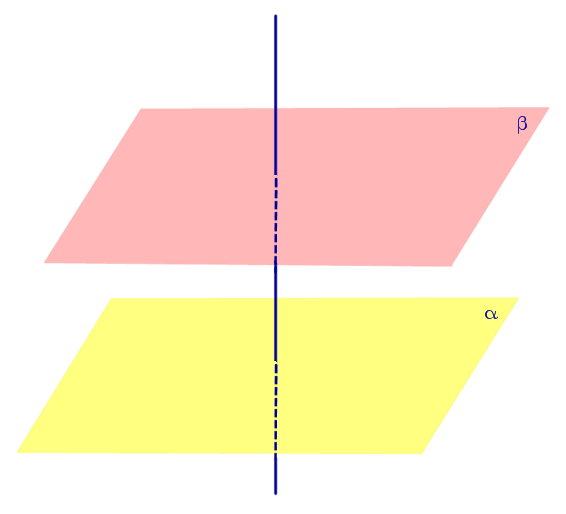
Свойство Плоскости, перпендикулярные к одной прямой, параллельны. |
| Признак перпендикулярности двух плоскостей |
|
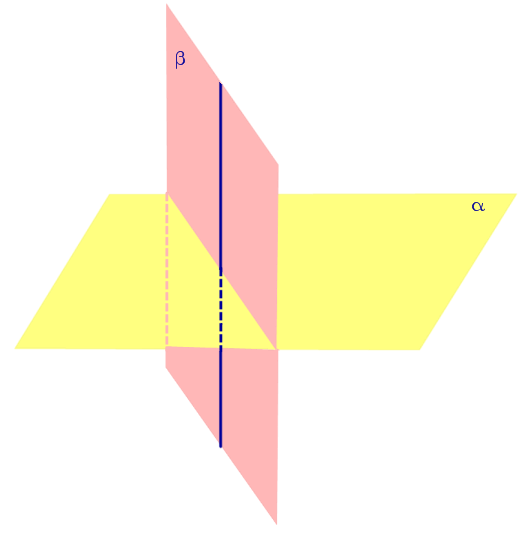
Признак Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны |
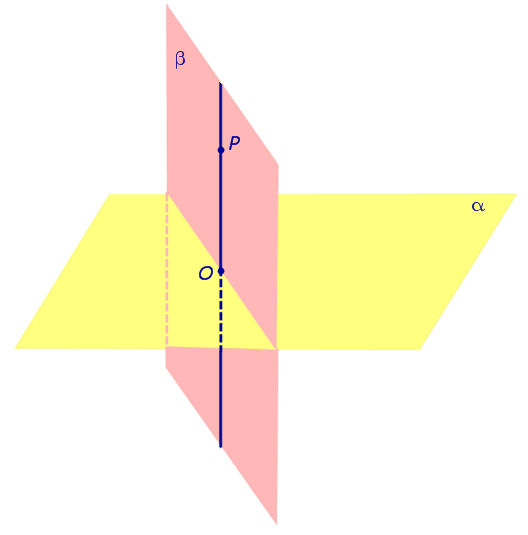
| Свойство перпендикуляра к плоскости |
|
Свойство Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β. |