Справочник по математике
Геометрия (Стереометрия) Прямые и плоскости в пространстве
Расстояние между двумя фигурами
Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.
| Определение расстояния между двумя точками |
|
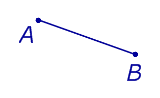
Определение Расстоянием между двумя точками A и B называют длину отрезка AB |
| Определение расстояния от точки, лежащей на прямой, до этой прямой |
|
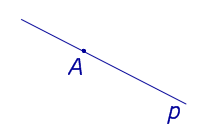
Определение Расстояние равно 0 |
| Определение расстояния от точки, не лежащей на прямой, до этой прямой |
|
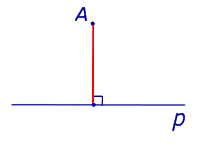
Определение Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую |
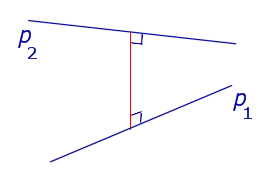
| Определение расстояния между двумя параллельными прямыми |
|
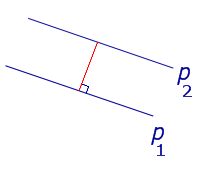
Определение Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую |
| Определение расстояния между двумя пересекающимися прямыми |
|
Определение Расстояние равно 0 |
| Определение расстояния между двумя скрещивающимися прямыми |
|
Определение Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым |
| Определение расстояния от точки, лежащей на плоскости, до этой плоскости |
|
Определение Расстояние равно 0 |
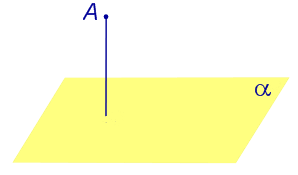
| Определение расстояния от точки, не лежащей на плоскости, до этой плоскости |
|
Определение Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость |
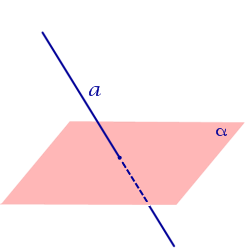
| Определение расстояния от прямой, пересекающей плоскость, до этой плоскости |
|
Определение Расстояние равно 0 |
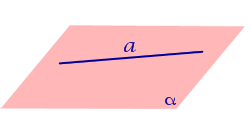
| Определение расстояния от прямой, лежащая на плоскости, до этой плоскости |
|
Определение Расстояние равно 0 |
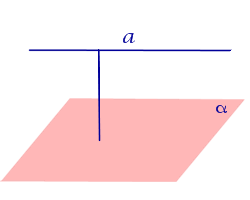
| Определение расстояния от прямой, параллельной плоскости, до этой плоскости |
|
Определение Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость |
| Определение расстояния между двумя пересекающимися плоскостями |
|
Определение Расстояние равно 0 |
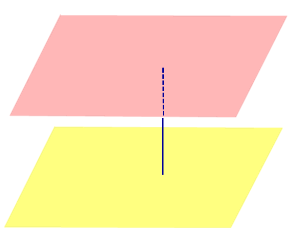
| Определение расстояния между двумя параллельными плоскостями |
|
Определение Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину) |
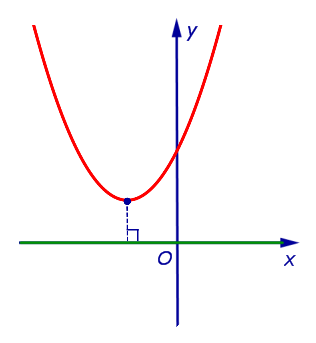
| Определение расстояния между параболой y = a x2 + b x + c, не пересекающей ось абсцисс, и осью абсцисс |
|
Определение Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс |
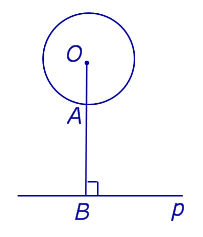
| Определение расстояния между окружностью и не пересекающей ее прямой |
|
Определение Расстоянием между окружностью и не переcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой. Если перпендикуляр OB, опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB. |
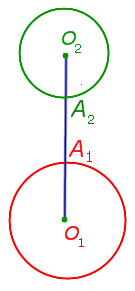
| Определение расстояния между двумя непересекающимися окружностями, каждая из которых лежит вне другой |
|
Определение Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2. |
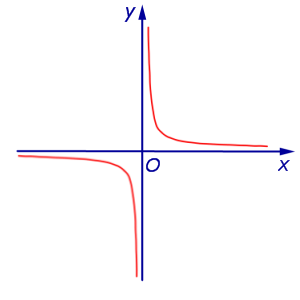
Определение расстояния между гиперболой 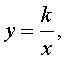 где k – любое, отличное от нуля, число, и осью абсцисс |
|
Определение Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой) |
