Справочник по математике

Геометрия (Стереометрия)

Прямые и плоскости в пространстве

Взаимное расположение прямой и плоскости в пространстве.
Признак параллельности прямой и плоскости

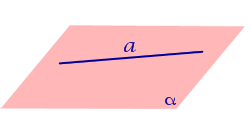
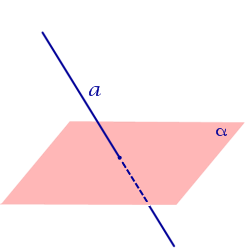
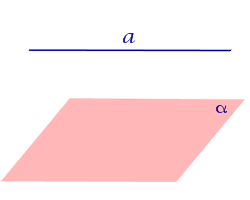
      Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.

Фигура	Рисунок	Формулировка
Прямая лежит на плоскости (принадлежит плоскости)		Прямая лежит на плоскости, если все точки прямой принадлежат плоскости. Замечание. Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.
Прямая пересекает плоскость		Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.
Прямая параллельна плоскости		Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

Прямая лежит на плоскости (принадлежит плоскости)

Прямая лежит на плоскости, если все точки прямой принадлежат плоскости. Замечание. Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.

Прямая пересекает плоскость

Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.

Прямая параллельна плоскости

Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

      Утверждение 1. Предположим, что прямая   a   и плоскость   α   параллельны, а плоскость   β   проходит через прямую   a .Тогда возможны два случая:

1. Плоскость   β  параллельна плоскости   α Плоскость   β  параллельна плоскости   α   (рис.1);
2. Плоскость   β   пересекает плоскость   α.   В этом случае прямая   b ,   которая является линией пересечения плоскостей   α   и   β ,   будет параллельна прямой   a прямая   b ,   которая является линией пересечения плоскостей   α   и   β ,   будет параллельна прямой   a   (рис.2).

Рис.1	Рис.2

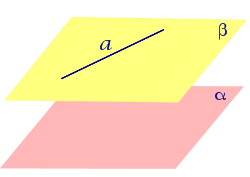
Рис.1

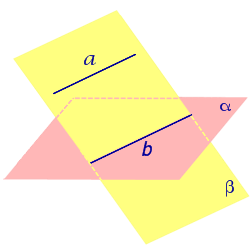
Рис.2

      Доказательство. Рассмотрим случай 2 и предположим противное. Предположим, что прямые   a   и   b   пересекаются в некоторой точке   P (рис.3) .

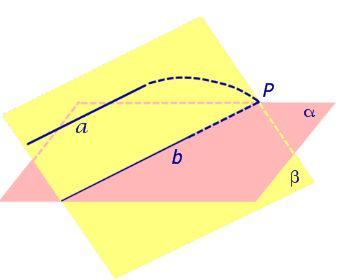
Рис.3

      Но тогда точка   P   оказывается точкой пересечения прямой   a   и плоскости   α ,   и мы получаем противоречие с тем, что прямая   a   и плоскость   α   параллельны. Полученное противоречие и завершает доказательство утверждения 1.

      Утверждение 2 (признак параллельности прямой и плоскости). Если прямая   a ,   не лежащая в плоскости   α ,   параллельна некоторой прямой   b,   лежащей в плоскости   α ,   то прямая   a   и плоскость   α  параллельны.

      Доказательство. Докажем признак параллельности прямой и плоскости "от противного". Предположим, что прямая   a   пересекает плоскость   α  в некоторой точке   P . Проведем плоскость   β   через параллельные прямые   a   и   b Проведем плоскость   β   через параллельные прямые   a   и   b   (рис. 4).

Рис.4

      Точка   P   лежит на прямой   a   и принадлежит плоскости   β.   Но по предположению точка   P   принадлежит и плоскости   α , следовательно точка   P   лежит на прямой   b ,   по которой пересекаются плоскости   α   и   β .   Однако прямые   a   и   b   параллельны по условию и не могут иметь общих точек.

      Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ по математике.