Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Конус, вписанный в пирамиду

Конус, вписанный в пирамиду. Свойства пирамиды, описанной около конуса

Отношение объемов конуса и описанной около него правильной n - угольной пирамиды

Конус, вписанный в пирамиду. Свойства пирамиды, описанной около конуса

      Определение 1. Конусом, вписанным в пирамиду, называют такой конус, у которого основание вписано в основание пирамиды, а вершина совпадает с вершиной пирамиды (рис. 1).

      Определение 2. Если конус вписан в пирамиду, то пирамиду называют описанной около конуса.

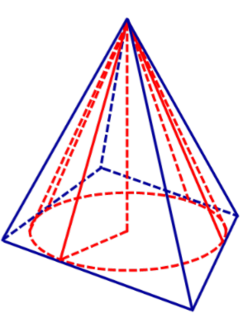
Рис.1

      Замечание. Высота конуса равна высоте пирамиды, описанной около него.

      Теорема 1. В пирамиду можно вписать конус тогда и только тогда, когда выполнены следующие два условия:

1. В основание пирамиды можно вписать окружность;
2. Основанием перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды, является центр вписанной в основание пирамиды окружности.

      Доказательство. Поскольку перпендикуляр, опущенный из вершины конуса на плоскость его основания, проходит через центр основания конуса, то для пирамиды, описанной около конуса, справедливость обоих условий теоремы вытекает из определения конуса, вписанного в пирамиду.

      Теперь рассмотрим пирамиду   SA₁A₂ ... A_n ,   для которой выполнены условия 1 и 2 теоремы, и докажем, что в нее можно вписать конус.

      Пусть   O   – центр круга, вписанного в основание   A₁A₂ ... A_n   пирамиды. Поскольку отрезок SO перпендикулярен плоскости основания пирамиды, то, соединив все точки этого круга с вершиной пирамиды   S  , мы получим конус с осью  OS,  вписанный в пирамиду   SA₁A₂ ... A_n   (рис. 2).

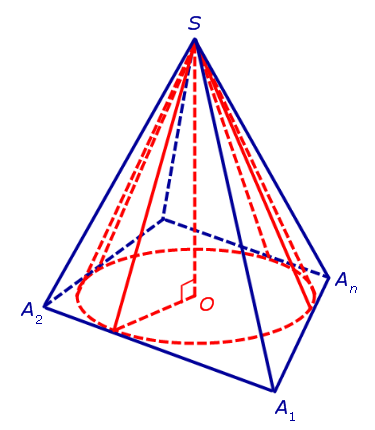
Рис.2

      Теорема доказана.

      Поскольку в любой правильный многоугольник можно вписать окружность, то из доказанной теоремы 1 непосредственно вытекает

       Следствие 1. В любую правильную пирамиду можно вписать конус.

       Теорема 2. Если у пирамиды   SA₁A₂ ... A_n   основание   O   перпендикуляра, опущенного из вершины   S   на плоскость основания пирамиды, лежит внутри многоугольника   A₁A₂ ... A_n ,   а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать конус.

      Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом   φ ,   а высота пирамиды равна   h.   Рассмотрим, например, боковую грань   SA₁A₂   и проведем в ней высоту   SB   (рис 3).

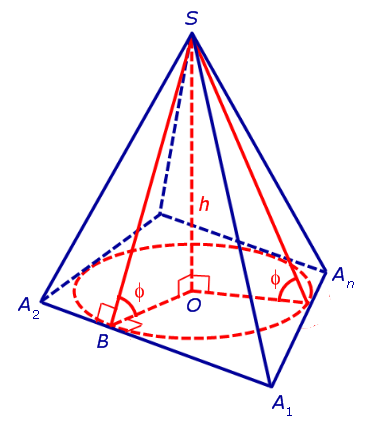
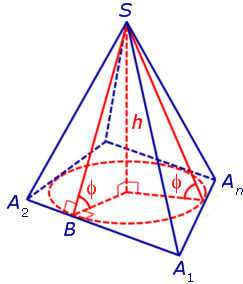
Рис.3

      По теореме о трех перпендикулярах отрезок   OB   перпендикулярен ребру   A₁A₂.   Следовательно, угол   SBO   является линейным углом двугранного угла между боковой гранью   SA₁A₂   и плоскостью основания пирамиды и равен   φ .   Катет   OB   прямоугольного треугольника   SOB   выражается через высоту пирамиды   h   и угол   φ   по формуле

OB = h ctg φ .

      Поскольку отрезок   OB   перпендикулярен ребру   A₁A₂,   то точка   O   удалена от прямой   A₁A₂   на расстояние точка   O   удалена от прямой   A₁A₂   на расстояние   h ctg φ .  Рассуждая аналогичным образом, получаем, что точка   O   удалена на расстояние   h ctg φ   от всех сторон многоугольника   A₁A₂ ... A_n .   Таким образом, точка   O   является центром окружности, вписанной в многоугольник   A₁A₂ ... A_n .   Радиус этой окружности равен   h ctg φ .   В то же время точка   O – основание перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды. По теореме 1 в такую пирамиду можно вписать конус.

       Доказательство теоремы 2 завершено.

Отношение объемов конуса и описанной около него правильной
n - угольной пирамиды

       Задача. Найти отношение объемов конуса и описанной около него правильной n - угольной пирамиды .

       Решение. Поскольку и объем конуса, и объем пирамиды вычисляются по формуле

,

а высота конуса равна высоте описанной около него пирамиды , то для объемов конуса и описанной около него правильной n - угольной пирамиды справедливо равенство

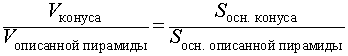
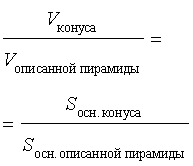
      Поскольку площадь правильного n - угольника выражается через радиус   r   вписанной в этот многоугольник окружности по формуле

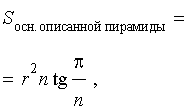
то справедливо равенство

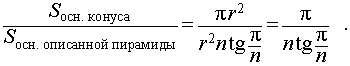
      Ответ.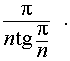

      Следствие 1. Отношение объема конуса к объему описанной около него правильной треугольной пирамиды равно

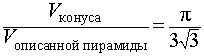
      Следствие 2. Отношение объема конуса к объему описанного около него правильного тетраэдра равно

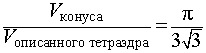
      Следствие 3. Отношение объема конуса к объему описанной около него правильной четырехугольной пирамиды равно

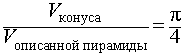
      Следствие 4. Отношение объема конуса к объему описанной около него правильной шестиугольной пирамиды равно

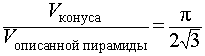
      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.