Квадратные уравнения
Квадратным трёхчленом относительно переменной 
называют многочлен
 , |
(1) |
где 
, 
и 
- произвольные вещественные числа, причем 
Квадратным уравнением относительно переменной называют уравнение
 |
(2) |
где , и - произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной называют уравнение
где , и - произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1. Решить уравнение
Решение.
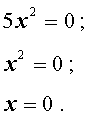
Ответ: 
.
Пример 2. Решить уравнение
 |
(3) |
Решение. Вынося в левой части уравнения (3) переменную за скобки, перепишем уравнение в виде
 |
(4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
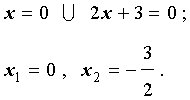
Ответ: 
.
Пример 3. Решить уравнение
Решение.
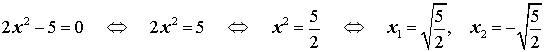
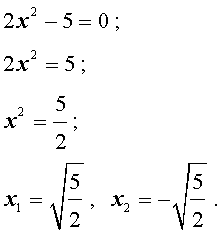
Ответ: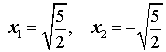 
.
Пример 4. Решить уравнение
 |
(5) |
Решение. Поскольку левая часть уравнения (5) положительна при всех значениях переменной , а правая часть равна 0, то уравнение решений не имеет.
Ответ: 
.
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
 |
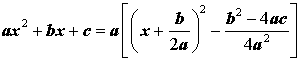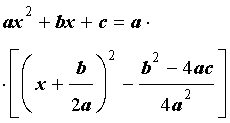(6) |
Для того, чтобы получить формулу (6), совершим следующие преобразования:
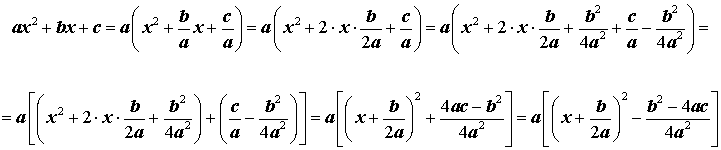
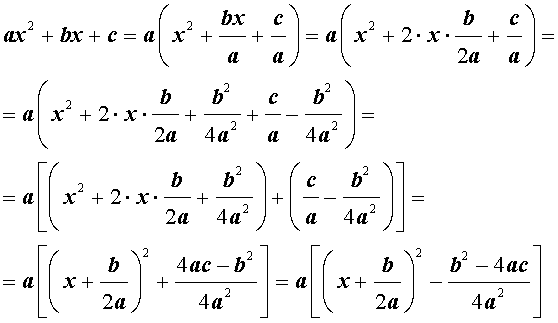
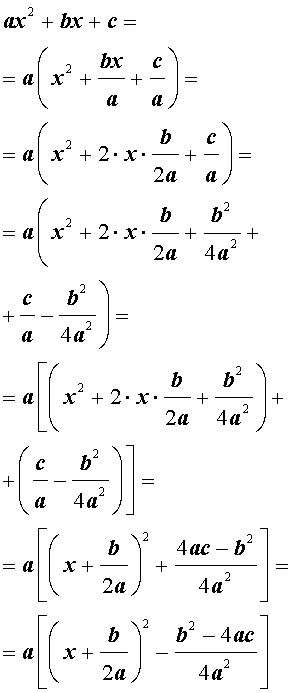
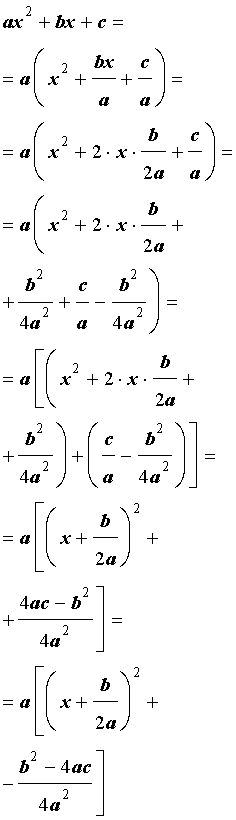
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой 
и вычисляется по формуле:
 |
(7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
 |
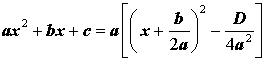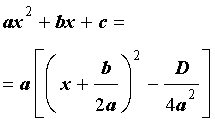(8) |
Разложение квадратного трёхчлена на множители
Утверждение. В случае, когда 
, квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда 
, квадратный трехчлен нельзя разложить на линейные множители.
Доказательство. В случае, когда 
, формула (8) и является разложением квадратного трехчлена на линейные множители:
 |
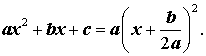(9) |
В случае, когда 
, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
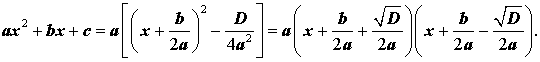
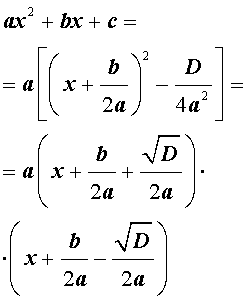
Таким образом, в случае, когда , разложение квадратного трехчлена (1) на линейные множители имеет вид
 |
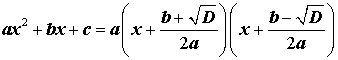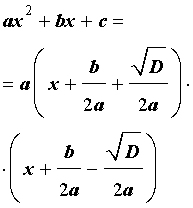(10) |
В случае, когда , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание. В случае, когда , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения.
Действительно, в случае, когда , из формулы (9) получаем:
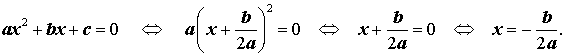
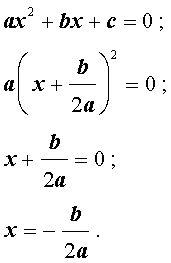
Следовательно, в случае, когда , уравнение (1) обладает единственным корнем, который вычисляется по формуле
 |
(11) |
В случае, когда , из формулы (10) получаем:
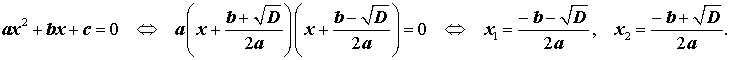
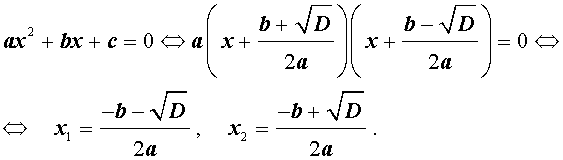
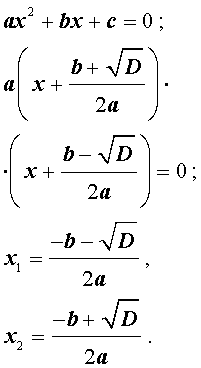
Таким образом, в случае, когда , уравнение (1) имеет два различных корня, которые вычисляются по формулам
 |
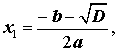(12) |
 |
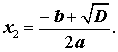(13) |
Замечание 1. Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
 |
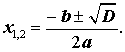(14) |
Замечание 2. В случае, когда , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда , квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
 |
(15) |
Замечание 3. В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
 |
(16) |
В случае, когда , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
 |
(17) |
Замечание 4. В случае, когда , корни 
и 
совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
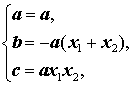
следствием которых являются формулы
 |
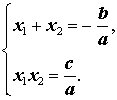(18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).
Словами прямая теорема Виета формулируется так: - «Если числа и являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: - «Если числа и являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика "проблемными".
Запись по телефону (495) 509-28-10. |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра "Резольвента" учебными материалами для подготовки к ЕГЭ и ГИА по математике.
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ГИА по математике, физике или русскому языку на высокий балл, учебный центр "Резольвента"
проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр "РЕЗОЛЬВЕНТА"
