Справочник по математике

Алгебра

Координатная плоскость

Парабола на координатной плоскости.
Решение квадратных неравенств

Парабола на координатной плоскости

Решение квадратных неравенств

Парабола на координатной плоскости

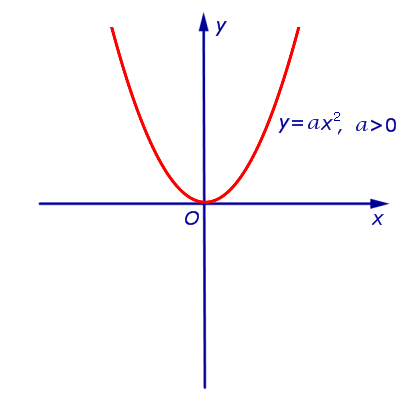
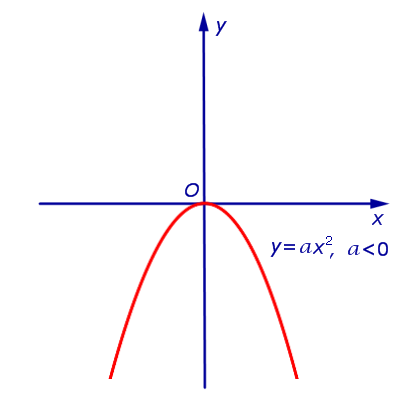
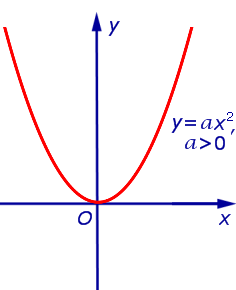
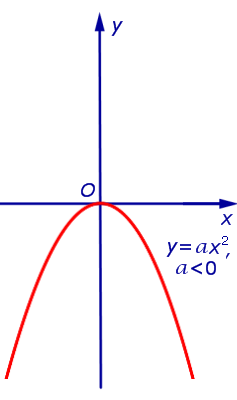
      Определение 1. Параболой называют график функции

где   a   – любое число, не равное нулю. Точку   О (0;0)   называют вершиной параболы (1).

      При   a > 0   и   a < 0   график функции (1) изображён на рисунках 1 и 2 соответственно.

Рис.1

Рис.2

Рис.1

Рис.2

      Функция (1) обладает следующими свойствами:

• областью определения функции функции (1) является вся числовая ось;
• функция (1) является четной функцией, поскольку для всех значений аргумента выполнено равенство

y (x) = y (– x) ;

• при   a > 0   функция (1) убывает на интервале 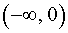    и возрастает на интервале   ;
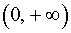  при   a < 0   функция (1) возрастает на интервале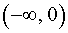     и убывает на интервале   ;
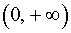• при   a > 0   у функции (1) существует единственный минимум на всей области определения, который достигается в точке   x = 0 ;
• при   a < 0   у функции (1) существует единственный максимум на всей области определения, который достигается в точке   x = 0 ;
• при   a > 0   ветви параболы (1) направлены вверх;
• при   a < 0   ветви параболы (1) направлены вниз;
• и при   a > 0,   и при   a < 0   вершиной параболы (1) является начало координат;
• и при   a > 0,   и при   a < 0   осью симметрии параболы (1) является ось ординат.

      Рассмотрим теперь функцию, заданную формулой

где   a,   b,   c   – любые числа, но число   a   не равно нулю.

      Поскольку выражение, стоящее в правой части формулы (2), является квадратным трёхчленом, то, в соответствии с материалом, изложенным в разделе «Квадратные уравнения», формулу (2) можно переписать в виде

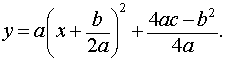(3)

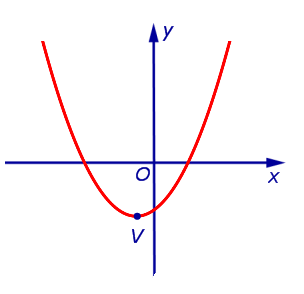
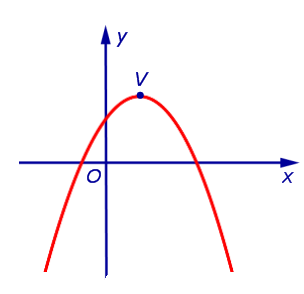
      Из формулы (3) вытекает, что график функции (2) может быть получен из графиков, изображенных на рисунках 1 или 2 (в зависимости от знака числа   a)   при помощи параллельного переноса, в результате которого вершина параболы (1) передвигается из начала координат в точку   V   (рис. 3, 4) с координатами

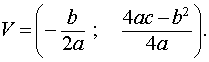(4)

Рис.3	Рис.4

Рис.3

Рис.4

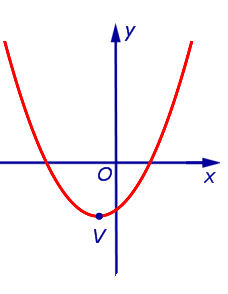Рис.3

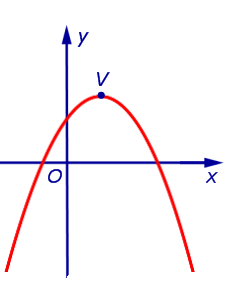Рис.4

      Поскольку дискриминант квадратного трёхчлена вычисляется по формуле

то координаты вершины параболы (3), определяемые по формуле (4), можно записать так:

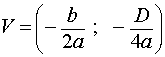(6)

      Замечание. При   a > 0   ветви параболы (2) направлены вверх, при   a < 0   ветви параболы (2) направлены вниз. Парабола (2) пересекает ось ординат в точке с координатами   (0; c).

Решение квадратных неравенств

      Зная расположение параболы (2) на координатной плоскости, можно, в частности, решать квадратные неравенства

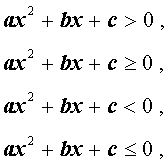
как показано в следующей таблице.

Знаки чисел   a   и   D a > 0,       D > 0 Корни уравнения a x2 + b x + c = 0 Два различных корня:   x1   и   x2 Расположение вершины Под осью   Ox Пересечения с осью   Ox В точках   x1   и   x2 Решение неравенства a x2 + b x + c > 0 Решение неравенства Решение неравенства a x2 + b x + c < 0 Решение неравенства

Знаки чисел   a   и   D a > 0,      D = 0 Корни уравнения a x2 + b x + c = 0 Два совпавших корня:   x1 = x2 Расположение вершины Лежит на оси   Ox Пересечения с осью   Ox Касается в точке   x1 Решение неравенства a x2 + b x + c > 0 Решение неравенства Решение неравенства a x2 + b x + c < 0 Решение неравенства x = x1

Знаки чисел   a   и   D a > 0,       D < 0 Корни уравнения a x2 + b x + c = 0 Корней нет Расположение вершины Над осью   Ox Пересечения с осью   Ox Не пересекает Решение неравенства a x2 + b x + c > 0 Решение неравенства Решение неравенства a x2 + b x + c < 0 Решение неравенства

Знаки чисел   a   и   D a < 0,       D > 0 Корни уравнения a x2 + b x + c = 0 Два различных корня:   x1   и   x2 Расположение вершины Над осью   Ox Пересечения с осью   Ox В точках   x1   и   x2 Решение неравенства a x2 + b x + c > 0 Решение неравенства Решение неравенства a x2 + b x + c < 0 Решение неравенства

Знаки чисел   a   и   D a < 0,       D = 0 Корни уравнения a x2 + b x + c = 0 Два совпавших корня:   x1 = x2 Расположение вершины Лежит на оси   Ox Пересечения с осью   Ox Касается в точке   x1 Решение неравенства a x2 + b x + c > 0 Решение неравенства x = x1 Решение неравенства a x2 + b x + c < 0 Решение неравенства

Знаки чисел   a   и   D a < 0,       D < 0 Корни уравнения a x2 + b x + c = 0 Корней нет Расположение вершины Под осью   Ox Пересечения с осью   Ox Не пересекает Решение неравенства a x2 + b x + c > 0 Решение неравенства Решение неравенства a x2 + b x + c < 0 Решение неравенства

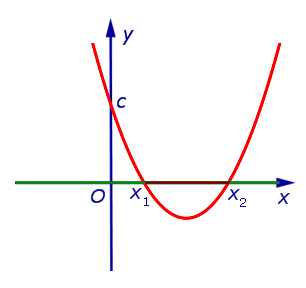
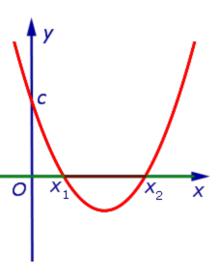
Знаки чисел   a   и   D: a > 0,       D > 0

Корни уравнения a x2 + b x + c = 0 :

два различных корня:   x1   и   x2

Расположение вершины:

под осью   Ox

Пересечения с осью   Ox :

в точках   x1   и   x2

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства :

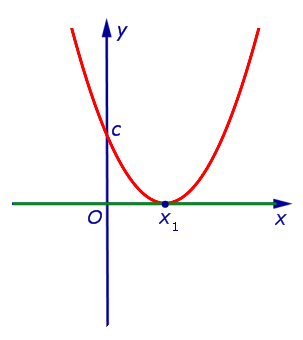
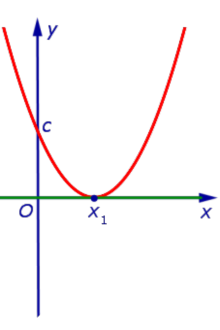
Знаки чисел   a   и   D: a > 0,      D = 0

Корни уравнения a x2 + b x + c = 0 :

два совпавших корня:   x1 = x2

Расположение вершины:

лежит на оси   Ox

Пересечения с осью   Ox :

касается в точке   x1

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства :

x = x1

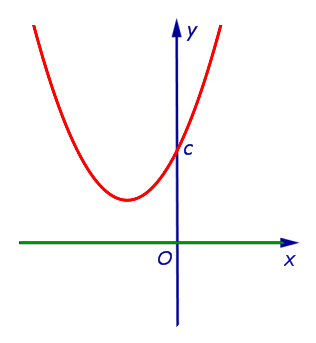
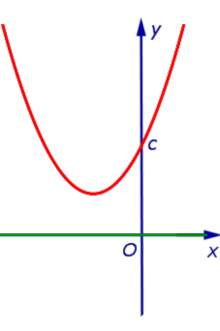
Знаки чисел   a   и   D: a > 0,       D < 0

Корни уравнения a x2 + b x + c = 0 :

корней нет

Расположение вершины:

над осью   Ox

Пересечения с осью   Ox :

не пересекает

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства :

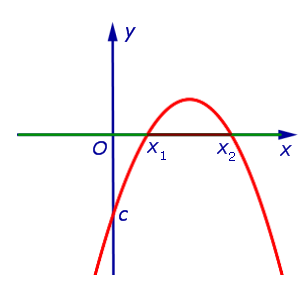
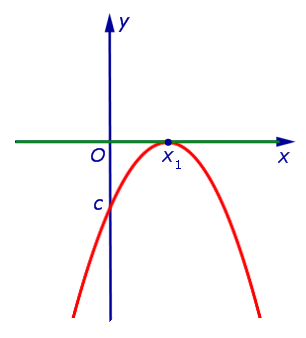
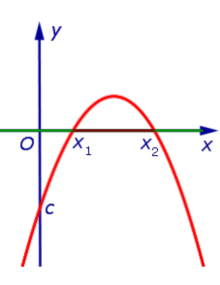
Знаки чисел   a   и   D: a < 0,       D > 0

Корни уравнения a x2 + b x + c = 0 :

два различных корня:   x1   и   x2

Расположение вершины:

над осью   Ox

Пересечения с осью   Ox :

в точках   x1   и   x2

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства

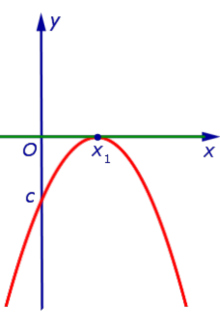
Знаки чисел   a   и   D: a < 0,       D = 0

Корни уравнения a x2 + b x + c = 0 :

два совпавших корня:   x1 = x2

Расположение вершины:

лежит на оси   Ox

Пересечения с осью   Ox :

касается в точке   x1

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

x = x1

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства

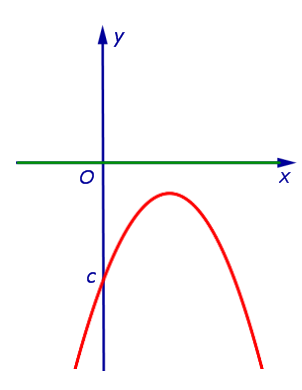
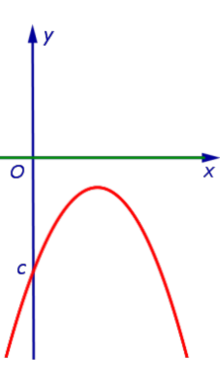
Знаки чисел   a   и   D: a < 0,       D < 0

Корни уравнения a x2 + b x + c = 0 :

корней нет

Расположение вершины:

под осью   Ox

Пересечения с осью   Ox :

не пересекает

Решение неравенства a x2 + b x + c > 0 :

Решение неравенства :

Решение неравенства a x2 + b x + c < 0 :

Решение неравенства :

      На нашем сайте можно также ознакомиться нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике.