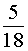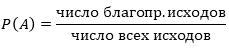Справочник по математикеТеория вероятностей и статистика Теория вероятностей

Классическое определение вероятности

Содержание

	Случайный эксперимент. Множество элементарных исходов. Случайные события
	Классическое определение вероятности
	Примеры решения задач

Случайный эксперимент. Множество элементарных исходов. Случайные события

Теория вероятностей - это раздел математики, посвященный изучению математических моделей случайных экспериментов, то есть таких экспериментов, результаты которых заранее неизвестны.

Например, одним из случайных экспериментов, часто используемых в теории вероятностей, является подбрасывание игральной кости. Результатом этого случайного эксперимента будет количество выпавших очков.

Напомним, что игральная кость – это кубик из однородного материала, грани которого пронумерованы числами   1, 2, 3, 4, 5, 6   при помощи нанесенных на грани кубика точек.

Множество всех возможных результатов случайного эксперимента называют множеством элементарных событий. Это множество принято обозначать заглавной греческой буквой   Ω .   Элементы множества   Ω   называют элементарными событиями.

Элементарные события часто называют элементарными исходами или, просто, исходами, а множество всех элементарных событий называют пространством элементарных событий, множеством элементарных исходов или пространством элементарных исходов.

В теории вероятностей случайными событиями являются подмножества множества элементарных исходов   Ω .   Например, в классическом определении вероятности событием является каждое подмножество множества элементарных событий   Ω.   В более сложных вероятностных моделях событиями являются не все подмножества   Ω,   а только часть из них.

Случайные события часто для простоты называют событиями.

Классическое определение вероятности

Если в результате случайного эксперимента может реализоваться один из нескольких равновозможных вариантов, то используют классическое определение вероятности.

Классическое определение вероятности является краеугольным камнем теории вероятностей и вводится в соответствии со следующей схемой.

1. Определяется множество элементарных событий (результаты случайного эксперимента).

   В классическом определении вероятности в качестве множества элементарных событий   Ω   используют произвольное множество, состоящее из конечного числа элементов. Элементы множества   Ω   (элементарные события) обозначают

   ω₁ ,  ω₂ , … , ω_N ,

   где   N   – число элементов множества   Ω .

2. Вероятность каждого элементарного события полагают равной

   

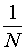
   и обозначают буквой   P .   Таким образом,

   

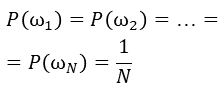
3. Определяются случайные события.

   Пустым множеством 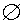    называют множество, в котором нет ни одного элемента. Пустое множество содержится в любом множестве, то есть является подмножеством любого множества.

   В классическом определении вероятности в качестве случайных событий используются всевозможные подмножества множества   Ω ,   включая пустое множество 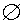и все множество   Ω .

   Случайные события принято обозначать буквами   A ,  B ,  C , ...

4. Определяется вероятность каждого случайного события.

   Если   A   – случайное событие, то вероятность события   A   полагают равной числу

   

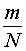
   где через   m   обозначено количество элементарных событий, входящих в множество   A .

   Вероятность случайного события   A   принято обозначать   P (A).

   Таким образом, справедливо равенство

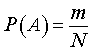
   (1)

   причем, поскольку числитель в правой части формулы (1) не превосходит знаменателя, то вероятность любого случайного события   A   заключена в пределах

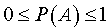
   (2)

   В частности, если 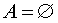    или   A = Ω ,   то справедливы равенства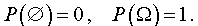

   (3)

ЗАМЕЧАНИЕ. При вычислении вероятности события   A   элементарные события, входящие в событие   A ,   называют благоприятными исходами и формулу (1) записывают в виде

Примеры решения задач

ПРИМЕР 1. Эксперимент состоит в подбрасывании игральной кости один раз. Описать схему введения классического определения вероятности для этого эксперимента.

РЕШЕНИЕ. Обозначим через   ω_k   событие, состоящее в том, что при подбрасывании игральной кости выпадает число   k .   Тогда элементарные события

составляют множество элементарных событий   Ω :

Поскольку множество   Ω   состоит из   6   элементов, то вероятность каждого элементарного события равна :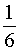

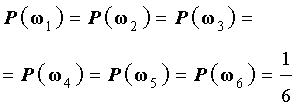
Каждое случайное событие является подмножеством   Ω   и состоит из нескольких элементарных событий. Так, например, случайное событие

A = { выпало нечетное число }

состоит из трех элементарных событий

A = {ω₁ ,  ω₃ ,  ω₅ } .

В силу формулы (4) справедливо равенство

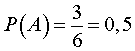
ПРИМЕР 2. Эксперимент состоит в подбрасывании монеты один раз. Описать схему введения классического определения вероятности для этого эксперимента.

РЕШЕНИЕ. Обозначим русскими буквами   Г   и   Ч   элементарные события, состоящие в том, что при подбрасывании монеты выпадают герб   ( Г )   или число   ( Ч )   соответственно. Тогда

Ω = { Г ,  Ч } ,

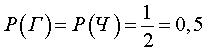
ПРИМЕР 3. Найти вероятность того, что при однократном подбрасывании двух игральных костей сумма выпавших чисел будет больше, чем   8 .

РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны всевозможные суммы чисел, выпавших при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании первой кости, а первый столбец таблицы – это числа, выпавшие при бросании второй кости. На пересечении строки и столбца указана сумма чисел, выпавших на двух костях.

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

В этой таблице все возможные результаты эксперимента представлены в   36   клетках. При этом в   10   клетках, выделенных в таблице желтым цветом, результаты превышают число   8 .   Поэтому искомая вероятность

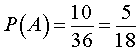
ОТВЕТ.