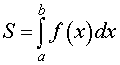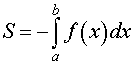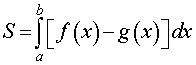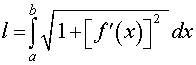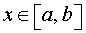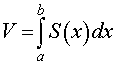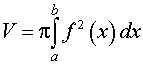Справочник по математике Элементы математического анализа
Элементы математического анализа Интегралы
Интегралы
Геометрические приложения определенного интеграла
Содержание

Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
В данном разделе справочника приведена таблица, содержащая формулы, с помощью которых можно вычислить:
-
Площади криволинейных трапеций различного вида (площади фигур, ограниченных графиками функций);
-
Длины дуг кривых на плоскости;
-
Объемы тел, если известны площади их поперечных сечений;
-
Объемы тел, полученных при вращении криволинейных трапеций вокруг оси абсцисс Ox ;
-
Площади поверхностей тел, полученных при вращении графиков функций вокруг оси абсцисс Ox.
|
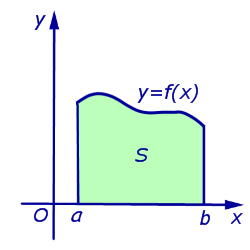
Площадь криволинейной трапеции, ограниченной сверху графиком функции y = f (x), f (x) > 0, a < x < b, снизу – осью Ox , а с боков – отрезками прямых x = a и x =b .
вычисляется по формуле:
|
|
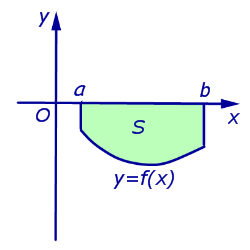
Площадь криволинейной трапеции, ограниченной сверху осью Ox , снизу – графиком функции y = f (x), f (x) < 0, a < x < b, а с боков – отрезками прямых x = a и x =b .
вычисляется по формуле:
|
|
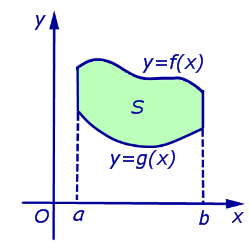
Площадь криволинейной трапеции, ограниченной сверху графиком функции y = f (x), a < x < b, снизу – графиком функции y = g (x), g (x) < f (x), a < x < b, а с боков – отрезками прямых x = a и x =b .
вычисляется по формуле:
|
|
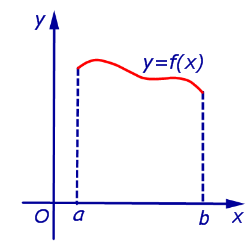
Длина дуги графика функции y = f (x), a < x < b,
вычисляется по формуле:
Эту формулу называют также формулой длины дуги кривой на плоскости. |
|
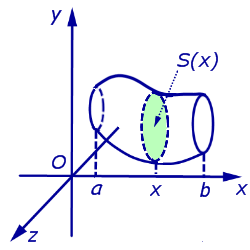
Объем тела в случае, когда площади поперечных сечений тела S (x), известны, причем плоскость каждого поперечного сечения перпендикулярна оси Ox,
вычисляется по формуле:
|
|
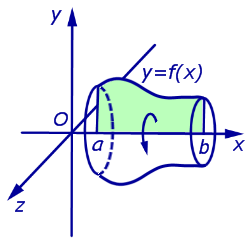
Объем тела, полученного при вращении криволинейной трапеции, ограниченной сверху графиком функции y = f (x), f (x) > 0, a < x < b, снизу – осью Ox , а с боков – отрезками прямых x = a и x =b , вокруг оси Ox
вычисляется по формуле:
Эту формулу называют также формулой объема тела вращения. |
|
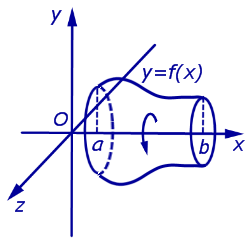
Площадь поверхности тела, полученного при вращении графика функции y = f (x), f (x) > 0, вокруг оси Ox
вычисляется по формуле:
Эту формулу называют также формулой площади поверхности тела вращения. |
Применение формул, перечисленных в таблице, проиллюстрировано на примерах, содержащих, в частности, вывод формулы объема пирамиды, формул объема шара и площади сферы.
Примеры решения задач на вычисление площадей фигур на плоскости
ПРИМЕР 1. Найти площадь фигуры, ограниченной линиями
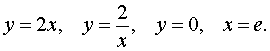
РЕШЕНИЕ. Рассматриваемая фигура (рис. 1) состоит из двух частей: треугольника OAB и криволинейной трапеции ABCD.
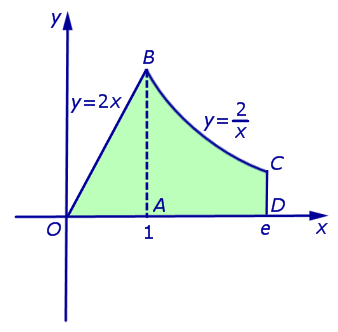
Рис.1
Дважды применим формулу для площади криволинейной трапеции с f (x) > 0, а затем вычислим полученные интегралы с помощью таблицы неопределенных интегралов и формулы Ньютона - Лейбница:
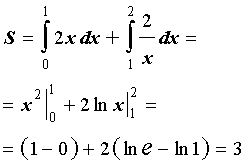
ОТВЕТ. 3.
ПРИМЕР 2. Найти площадь криволинейной трапеции, изображенной на рисунке 2
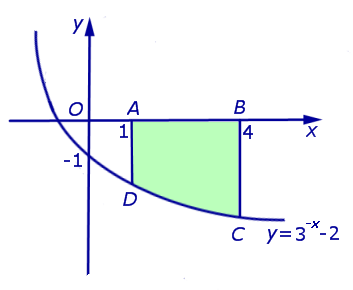
Рис.2
РЕШЕНИЕ. Площадь криволинейной трапеции ABCD вычисляется с помощью формулы для площади криволинейной трапеции с f (x) < 0:
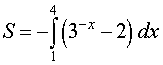 .
.
Воcпользовавшись таблицей неопределенных интегралов и формулой Ньютона - Лейбница, находим
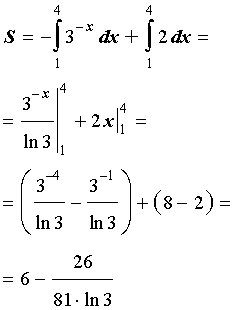
ОТВЕТ. 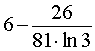 .
.
Пример решения задачи на вычисление длины дуги кривой на плоскости
ПРИМЕР 3 . Найти длину дуги графика функции
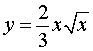 , 8 < x < 15 .
, 8 < x < 15 .
РЕШЕНИЕ. График рассматриваемой функции изображен на рисунке 3
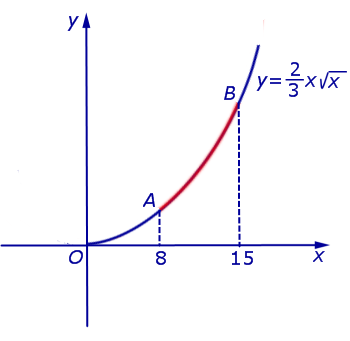
Рис.3
Для вычисления длины дуги AB нужно, в соответствии с формулой для длины дуги графика функции, вычислить определенный интеграл
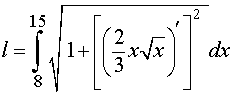 |
(1) |
Воспользовавшись свойствами степеней и таблицей производных, находим
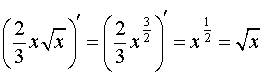
Подставим найденную производную в формулу (1), а затем вычислим полученные интегралы при помощи таблицы неопределенных интегралов и формулы Ньютона - Лейбница:
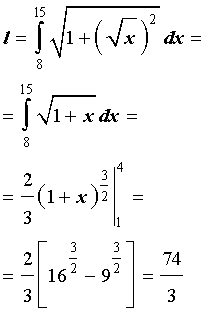
ОТВЕТ. 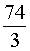
Вывод формул для объема пирамиды и для объема шара
ПРИМЕР 4. Вывести формулу для объема пирамиды, воспользовавшись формулой для вычисления объема тела по известным площадям поперечных сечений.
РЕШЕНИЕ. Рассмотрим произвольную n - угольную пирамиду BA1A2 ... An с вершиной B, высота BK которой равна H, а площадь основания A1A2 ... An равна S. Обозначим через S (x) площадь сечения 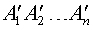 этой пирамиды плоскостью, параллельной основанию пирамиды и находящейся на расстоянии x от вершины пирамиды B (рис. 4).
этой пирамиды плоскостью, параллельной основанию пирамиды и находящейся на расстоянии x от вершины пирамиды B (рис. 4).
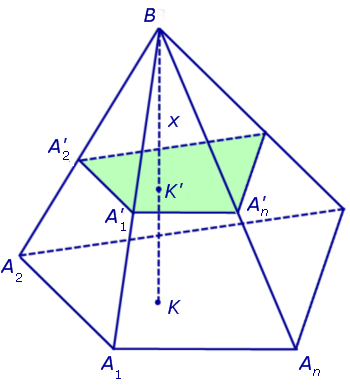
Рис.4
Поскольку многоугольники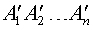 и A1A2 ... An подобны с коэффициентом подобия
и A1A2 ... An подобны с коэффициентом подобия 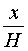 , то площади этих многоугольников удовлетворяют равенству
, то площади этих многоугольников удовлетворяют равенству
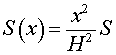 |
(2) |
Рассмотрим теперь в пространстве систему координат Oxyz и расположим нашу пирамиду BA1A2 ... An так, чтобы ее вершина B совпала с началом координат O, а высота пирамиды BK оказалась лежащей на оси Ox (рис. 5).
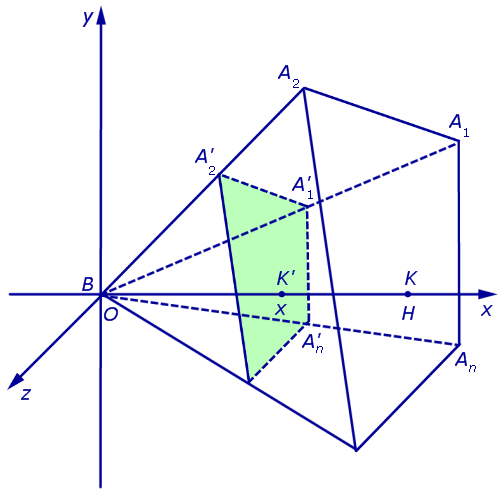
Рис.5
Тогда сечение 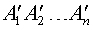 пирамиды и будет поперечным сечением, поскольку его плоскость перпендикулярна оси Ox.
пирамиды и будет поперечным сечением, поскольку его плоскость перпендикулярна оси Ox.
Воспользовавшись формулой, позволяющей вычислить объем тела по известным площадям поперечных сечений, получаем
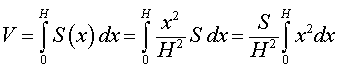
Далее при помощи таблицы неопределенных интегралов и формулы Ньютона - Лейбница находим
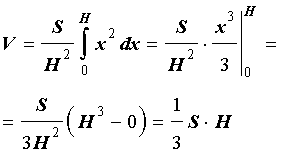
Итак, мы получили формулу для объема пирамиды
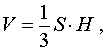
которой пользовались в различных разделах справочника.
ЗАМЕЧАНИЕ. Совершенно аналогично выводится формула для объема конуса. Формулы для объема прямой призмы и для объема цилиндра вывести таким способом еще проще, поскольку у них все сечения, перпендикулярные высоте, равны между собой. Мы рекомендуем провести эти выводы читателю самостоятельно в качестве полезного упражнения.
ПРИМЕР 5. Вывести формулу для объема шара радиуса R, воспользовавшись формулой для вычисления объема тела вращения.
РЕШЕНИЕ. Рассмотрим функцию
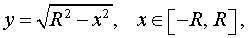 |
(3) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O. Шар радиуса R получается в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции (3) и ограниченной снизу отрезком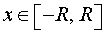 оси Ox (рис. 6).
оси Ox (рис. 6).
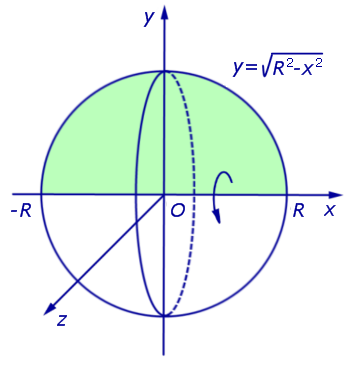
Рис.6
В соответствии с формулой для вычисления объема тела вращения получаем
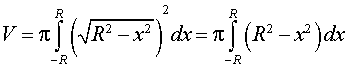
Далее при помощи таблицы неопределенных интегралов и формулы Ньютона - Лейбница находим
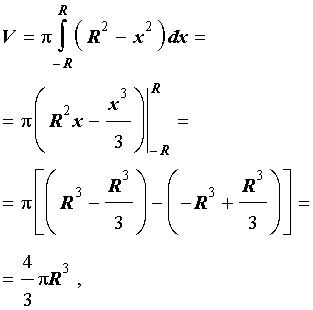
что и должно было получиться.
Вывод формулы для площади сферы
ПРИМЕР 6. Вывести формулу для площади сферы радиуса R, воспользовавшись формулой для вычисления площади поверхности тела вращения.
РЕШЕНИЕ. Снова рассмотрим функцию
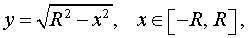 |
(4) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O (рис. 7).

Рис.7
Поскольку сфера радиуса R получается в результате вращения вокруг оси Ox графика функции (4), то в соответствии с формулой для вычисления площади поверхности тела вращения получаем
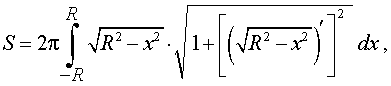
Воспользовавшись свойствами степеней, таблицей производных сложных функций и таблицей производных часто встречающихся функций, находим
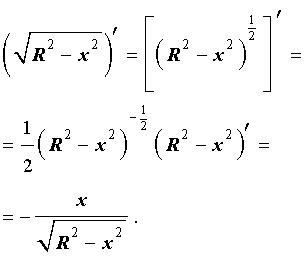
Подставим найденную производную в выражение, стоящее под знаком квадратного корня:
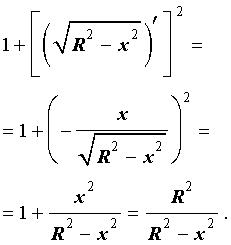
Таким образом, подынтегральная функция принимает вид:
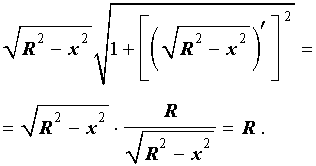
Далее с помощью таблицы неопределенных интегралов и формулы Ньютона - Лейбница получаем
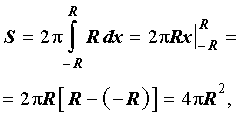
что и должно было получиться.
Близкие по тематике разделы сайта
С более подробным и расширенным изложением материала «Интегральное исчисление функций одной переменной» можно ознакомиться в учебно-методическом пособии: «Интегральное исчисление функций одной переменной».
Способы вычисления неопределенных интегралов можно посмотреть также в пособиях
- «Неопределенный интеграл. Простейшие приемы интегрирования»,
- «Интегрирование рациональных дробей»,
- «Интегрирование иррациональных функций»,
- «Интегрирование выражений, содержащих тригонометрические и гиперболические функции»
на странице «Учебные материалы по математическому анализу для студентов МФТИ (1 курс, 2 семестр)».