Справочник по математике

Алгебра

Степени и корни

Степень с рациональным показателем

Свойства степеней с рациональными показателями

Понятие о степени с иррациональным показателем

      Пусть p – произвольное положительное рациональное число. Тогда это рациональное число можно представить в виде несократимой дроби

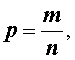
где m и n – натуральные числа. Предположим также, что a – произвольное положительное действительное число.

      Теперь мы можем дать определение степени с рациональным показателем.

      Определение. Степень, показатель которой есть положительное рациональное число, определяется по формуле:

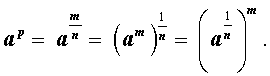
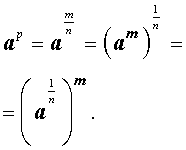
      Определение. Степень, показатель которой есть отрицательное рациональное число, определяется по формуле:

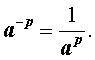
      Определение. Степень с нулевым показателем определяется по формуле:

a⁰ = 1 .

      Пример.

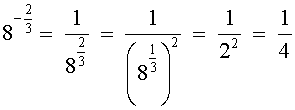
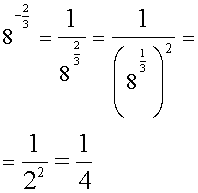
Свойства степеней с рациональными показателями

      Для степеней с рациональными показателями выполняются следующие свойства:

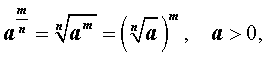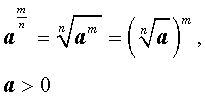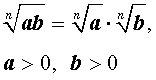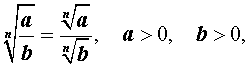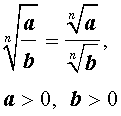      Кроме того, если   p   и   q   – произвольные рациональные числа, то

	a p a q = a p + q,       a > 0 ,
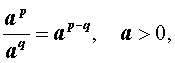	(a p ) q = a pq,       a > 0 ,
	(ab) p = a p b q,       a > 0 ,       b > 0 ,

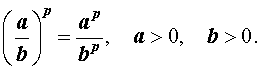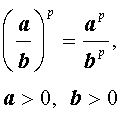      Замечание. Желающие могут ознакомиться с нашей презентацией  «Степень с рациональным показателем», содержание которой связано с данным разделом.

Понятие о степени с иррациональным показателем

      Кроме степеней с рациональными показателями в математике и других точных науках большое значение имеют и степени с иррациональными показателями, однако их определение выходит за рамки курса средней школы. Упомянем лишь о том, что степень с иррациональным показателем строится с помощью предельного перехода по последовательностям степеней с рациональными показателями, которые являются приближениями иррационального показателя степени с недостатком и с избытком.

      С понятиями степени с целочисленным показателем и арифметического корня можно ознакомиться в разделе «Степень с целочисленным показателем и арифметический корень» нашего справочника.

      Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.