Декартовы координаты точек плоскости. Уравнение окружности
 Числовая ось Числовая ось |
 Прямоугольная декартова система координат на плоскости Прямоугольная декартова система координат на плоскости |
 Формула для расстояния между двумя точками координатной плоскости Формула для расстояния между двумя точками координатной плоскости |
 Уравнение окружности на координатной плоскости Уравнение окружности на координатной плоскости |
Числовая ось
Определение 1. Числовой осью (числовой прямой, координатной прямой) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
O → x
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
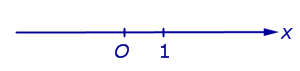
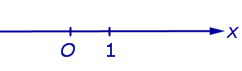
Рис.1
Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.
Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3. Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
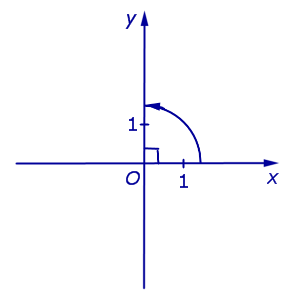
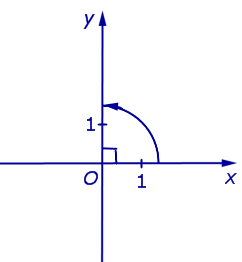
Рис.2
Замечание. Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат, в отличие от левых систем координат, в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
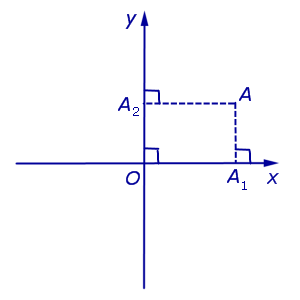
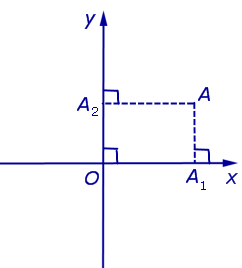
Рис.3
Определение 4. Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение. Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
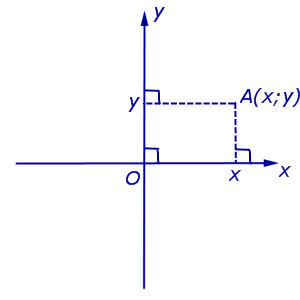
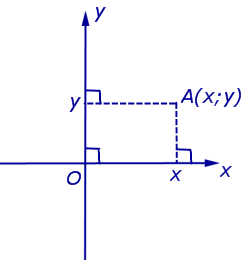
Рис.4
Замечание. Точка O , называемая началом координат, имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс, а числовую ось Oy называют осью ординат (рис. 5).
Определение 6. Каждая прямоугольная декартова система координат делит плоскость на 4 четверти (квадранта), нумерация которых показана на рисунке 5.
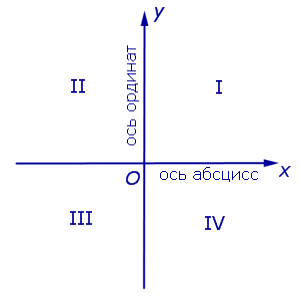
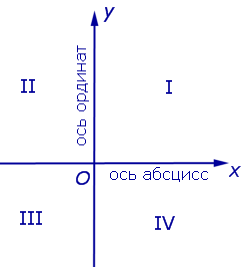
Рис.5
Определение 7. Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью.
Замечание. Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1. Расстояние между двумя точками координатной плоскости
A1 (x1 ; y1) и A2 (x2 ; y2)
вычисляется по формуле
![]()
Доказательство. Рассмотрим рисунок 6.
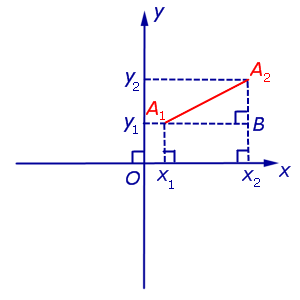
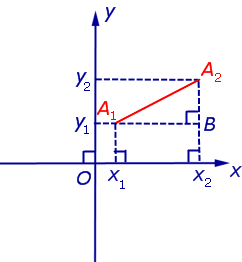
Рис.6
Поскольку в прямоугольном треугольнике A1A2B длина катета A1B равна | x2 – x1| а длина катета A2B равна | y2 – y1| , то по теореме Пифагора
| | A1A2|2 = = ( x2 – x1)2 + ( y2 – y1)2 . | (1) |
Следовательно,
![]()
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Рассмотрим на координатной плоскости Oxy (рис. 7) окружность радиуса R с центром в точке A0 (x0 ; y0) .
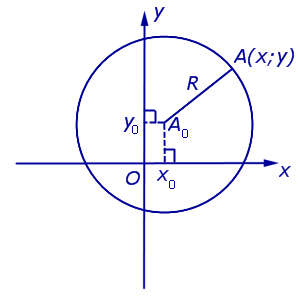
Рис.7
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
( x – x0)2 + ( y – y0)2 = R2.
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие. Уравнение окружности радиуса R с центром в начале координат имеет вид
x2 + y2 = R2.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
