Возвратные последовательности:
рекуррентная формула, характеристическое уравнение
Определение возвратной последовательности
Существуют два способа задания числовых последовательностей – с помощью формулы общего члена последовательности и с помощью рекуррентной формулы.
Например, геометрическую прогрессию
x1 , x2 , … xn , …
можно задать, как с помощью формулы общего члена
xn = b1q n – 1,
n = 1, 2, 3, … ,
так и с помощью рекуррентной формулы
x1 = b1; xn = q xn – 1,
n = 2, 3, …,
в каждой из которых символами b1 и q обозначены заданные числа – первый член и знаменатель прогрессии.
Определение. Пусть k – натуральное число. Возвратной (рекуррентной) последовательностью порядка k называют последовательность, для задания которой требуется задать первые её k членов, т.е. числа
x1 , x2 , … xk ,
а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)
xn = q1 xn – 1 + q2 xn – 2 +
+ … + qk xn – k ,
n > k ,
где
q1 , q2 , … qk ,
– заданные числа (коэффициенты рекуррентной формулы).
Замечание 1. Числа
x1 , x2 , … xk ,
называют начальными условиями.
Замечание 2. Для упрощения вычислений везде в дальнейшем будем рассматривать только случай возвратных последовательностей 2-го порядка, все члены которых являются вещественными числами.
Для задания таких последовательностей требуется задать их первые два члена, то есть вещественные числа x1 и x2, а остальные члены последовательности
x1 , x2 , … xn , …
определяются с помощью рекуррентной формулы
| xn = q1 xn – 1 + q2 xn – 2 , n > 2 , | (1) |
где q1, q2 – заданные вещественные числа.
Характеристическое уравнение
Для того, чтобы получить характеристическое уравнение возвратной последовательности (1), будем искать такие числа λ, при которых последовательность вида
| xn = λn | (2) |
удовлетворяет рекуррентной формуле (1).
Поскольку
| xn – 1 = λn – 1 , xn – 2 = λn – 2 , | (3) |
то при подстановке формул (2) и (3) в формулу (1) возникает уравнение
λn = q1 λn – 1 + q2 λn – 2 ,
которое удобно переписать в виде
| λn – q1 λn – 1 – – q2 λn – 2 = 0 . | (4) |
Если теперь уравнение (4) разделить на λn–2, то мы получим квадратное уравнение относительно λ вида:
λ2 – q1 λ – q2 = 0 ,
которое и называют характеристическим уравнением.
Общее решение рекуррентного уравнения второго порядка
В случае, когда характеристическое уравнение имеет два различных вещественных корня λ1 и λ2 , каждая из последовательностей
![]()
и ![]()
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
![]()
также удовлетворяет рекуррентной формуле (1).
Числа c1 и c2 называют произвольными постоянными.
В случае, когда характеристическое уравнение имеет два совпавших вещественных корня λ1 = λ2, непосредственная проверка показывает, что каждая из последовательностей
![]()
и ![]()
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
![]()
также удовлетворяет рекуррентной формуле (1).
В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ1, 2 = α ± i β, каждая из последовательностей
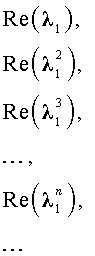
и
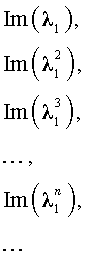
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
![]()
также удовлетворяет рекуррентной формуле (1).
![]()
Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |

