Возвратные последовательности: вывод формулы общего члена
Схема вывода формулы общего члена возвратной последовательности второго порядка
Определения возвратной последовательности, рекуррентной формулы, характеристического уравнения и формулы для общего решения рекуррентных уравнений приведены в разделе «Возвратные последовательности: рекуррентная формула, характеристическое уравнение» нашего справочника.
Целью данного раздела является получение формулы общего члена возвратной последовательности второго порядка. Вывод этой формулы состоит из 5 этапов:
- Вычисление корней характеристического уравнения возвратной последовательности.
- Нахождение общего решения рекуррентного уравнения в случае, когда характеристическое уравнение имеет:
- два различных вещественных корня,
- два совпавших вещественных корня,
- два комплексно сопряженных корня.
- Составление с помощью начальных условий системы из двух линейных уравнений с двумя неизвестными для нахождения двух произвольных постоянных.
- Решение системы уравнений для нахождения двух произвольных постоянных.
- Выписывание формулы общего члена возвратной последовательности.
Примеры с решениями
Пример 1. Найти формулу общего члена последовательности, заданной рекуррентной формулой
| xn = 6 xn – 1 – 5 xn – 2 , n > 2 , | (1) |
с начальными условиями
| x1 = 2, x2 = 1 . | (2) |
Решение. Будем действовать в соответствии со схемой.
Характеристическое уравнение для последовательности (1) имеет вид
λ2 – 6 λ + 5 = 0 .
λ1 = 5 , λ2 = 1 .
Поскольку корни характеристического уравнения вещественные и различные, то общее решение рекуррентного уравнения (1) имеет вид
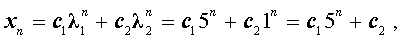
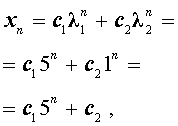
где c1 и c2 – произвольные действительные числа.
Найдем теперь значения произвольных постоянных c1 и c2 так, чтобы для последовательности
xn = c15n + c2 (3) выполнялись начальные условия (2). Это означает, что числа c1 и c2 должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными :
Решим полученную систему уравнений:
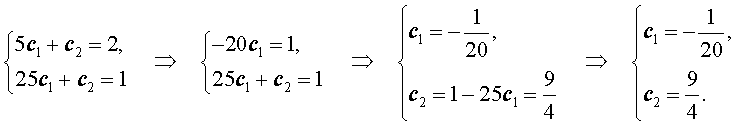
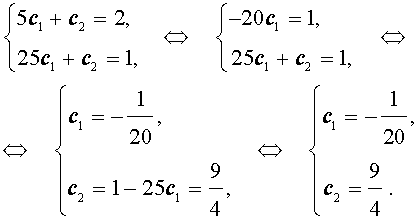
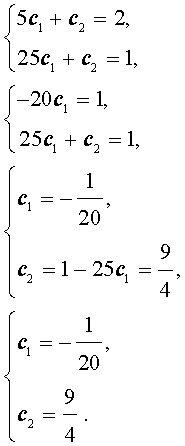
Подставляя найденные значения произвольных постоянны c1 и c2 в формулу (3), получаем искомую формулу общего члена последовательности:
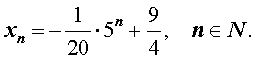
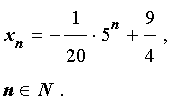
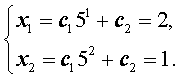
Решение примера 1 закончено.
Пример 2. Найти формулу общего члена последовательности, заданной рекуррентной формулой
| xn = 4 xn – 1 – 4 xn – 2 , n > 2 , | (4) |
с начальными условиями
| x1 = 1, x2 = 3 . | (5) |
Решение. Будем действовать в соответствии со схемой.
Характеристическое уравнение для последовательности (4) имеет вид
λ2 – 4 λ + 4 = 0 .
λ1 = λ2 = 2 .
Поскольку корни характеристического уравнения вещественны и равны между собой, то общее решение рекуррентного уравнения (4) имеет вид
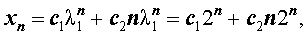
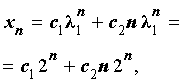
где c1 и c2 - произвольные вещественные числа.
Найдем теперь значения произвольных постоянных c1 и c2 так, чтобы для последовательности
xn = c12n + c2 n 2n (6) выполнялись начальные условия (5). Это означает, что числа c1 и c2 должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными :
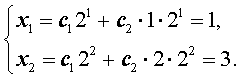
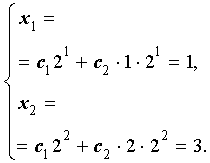
Решим полученную систему уравнений:
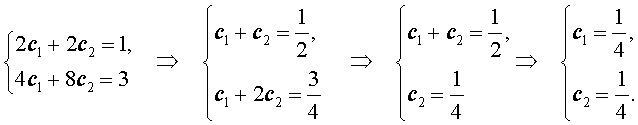
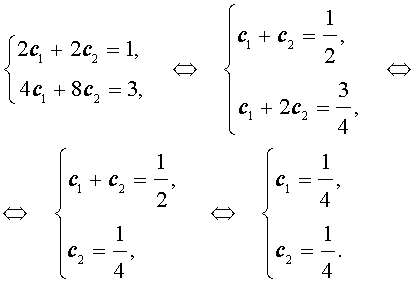
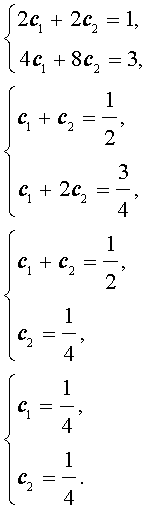
Подставляя найденные значения произвольных постоянных c1 и c2 в формулу (6), получаем искомую формулу общего члена последовательности:
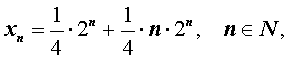
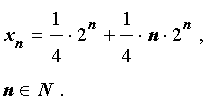
которую удобно переписать в виде:
xn = (1 + n) 2n – 2,
n = 1, 2, …
Решение примера 2 закончено.
Пример 3. Найти формулу общего члена последовательности, заданной рекуррентной формулой
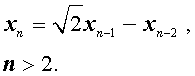 | (7) |
с начальными условиями
| (8) |
Решение. Будем действовать в соответствии со схемой.
Характеристическое уравнение для этой последовательности имеет вид
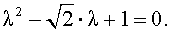
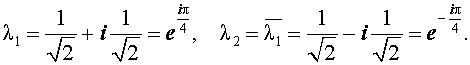
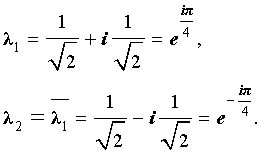
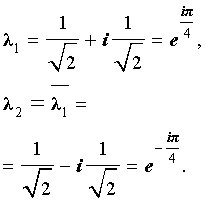
Поскольку характеристическое уравнение имеет два комплексно сопряженных корня, то общее решение рекуррентного уравнения (7) имеет вид
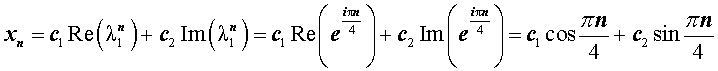 ,
,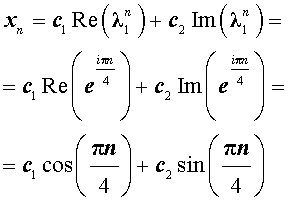
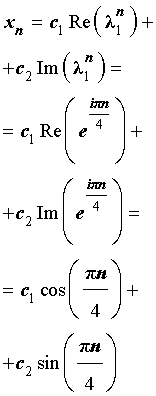
где c1 и c2 - произвольные вещественные числа.
Найдем теперь значения произвольных постоянных c1 и c2 так, чтобы для последовательности
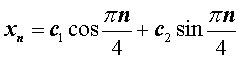
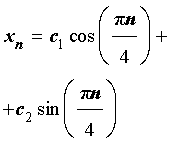
(9) выполнялись начальные условия (8). Это означает, что числа c1 и c2 должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными :
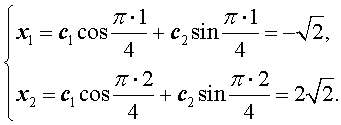
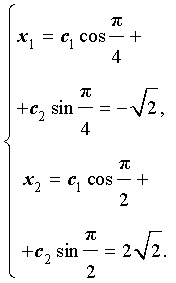
Для того, чтобы решить эту систему уравнений, перепишем её в следующем виде:
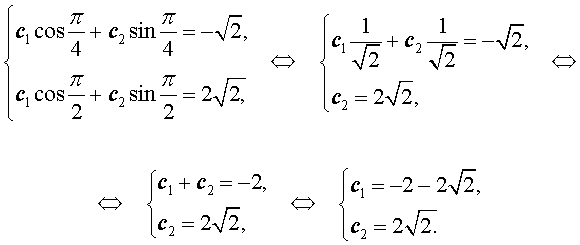
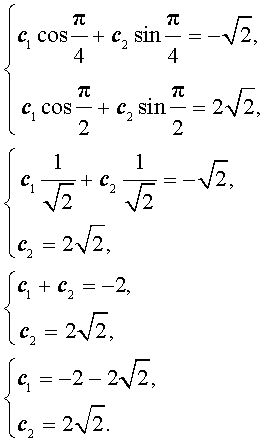
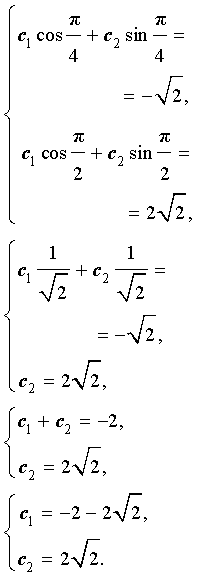
Подставляя найденные значения произвольных постоянных c1 и c2 в формулу (9), получаем искомую формулу общего члена последовательности:
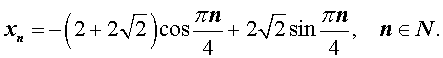
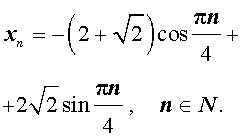
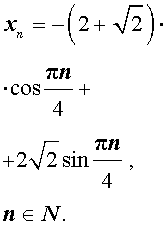
Решение примера 3 закончено.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |

