Геометрическая прогрессия
Определение 1. Числовую последовательность
все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства
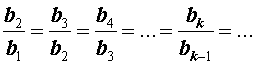
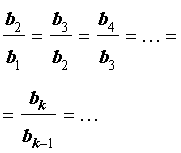
Определение 2. Если последовательность чисел
является геометрической прогрессией, то число 
, определенное формулой
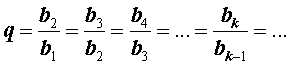
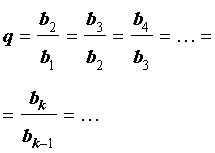
называют знаменателем этой геометрической прогрессии.
Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии 
и знаменатель геометрической прогрессии . Если числа и известны, то все остальные члены прогрессии можно найти по формулам:
 |
(1) |
По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел и .
Из формул (1) вытекает общая формула
 |
(2) |
позволяющая по любому номеру 
вычислить член 
геометрической прогрессии, зная первый член и знаменатель прогрессии. Эта формула носит название формулы общего члена геометрической прогрессии.
Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: - «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при 
справедливо равенство
 |
(3) |
В случае, когда
и 
все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:
 |
(4) |
Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.
Если для суммы первых членов геометрической прогрессии ввести обозначение
то при 
будет справедливо равенство
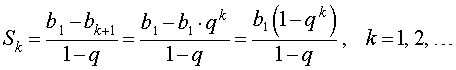
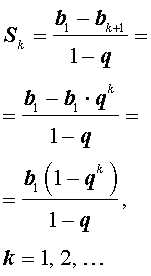
которое называется формулой для суммы первых 
членов геометрической прогрессии.
В случае, когда 
, все члены геометрической прогрессии равны, что не представляет особого интереса.
Бесконечно убывающая геометрическая прогрессия
Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству
В этом случае выполнено равенство
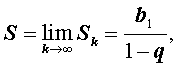
а величину 
называют суммой бесконечно убывающей геометрической прогрессии.
С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра "Резольвента" учебными материалами для подготовки к ЕГЭ и ГИА по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика "проблемными".
Запись по телефону (495) 509-28-10. |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ГИА по математике, физике или русскому языку на высокий балл, учебный центр "Резольвента"
проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр "РЕЗОЛЬВЕНТА"
