Задачи на смеси, сплавы и растворы
 Концентрация (процентное содержание) вещества Концентрация (процентное содержание) вещества |
 Примеры решения задач на смеси, сплавы и растворы Примеры решения задач на смеси, сплавы и растворы |
Концентрация (процентное содержание) вещества
Рассмотрим смесь (сплав, раствор) из нескольких веществ.
Определение 1. Концентрацией (процентной концентрацией, процентным содержанием) вещества A в смеси (сплаве, растворе) называют число процентов pA , выраженное формулой
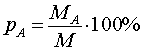 | (1) |
где MA – масса вещества A в смеси (сплаве, растворе), а M – масса всей смеси (сплава, раствора).
Часто в задачах на растворы указаны не массы входящих в них веществ, а их объёмы. В этом случае вместо формулы (1) для концентрации (процентной концентрации, процентного содержания) вещества A в растворе используется формула
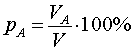 | (2) |
где VA , – объём вещества А в растворе, а V – объем всего раствора.
Определение 2. Формулу (1) называют формулой для массовой концентрации вещества A в смеси (сплаве, растворе), а формулу (2) – формулой для объёмной концентрации вещества A в растворе.
При решении задач считается, что при слиянии нескольких растворов (сплавов) масса и объем полученной смеси равны сумме масс и объемов смешиваемых компонентов соответственно.
Приёмы, используемые при решении задач на массовые концентрации смесей (сплавов, растворов), а также при решении задач на объёмные концентрации растворов, являются общими, что мы и увидим при решении следующих типовых задач
Примеры решения задач на смеси, сплавы и растворы
Задача 1. Смешали 16 литров 30% раствора кислоты в воде с 9 литрами 80% раствора кислоты в воде. Найти концентрацию полученного раствора кислоты в воде.
Решение. В 16 литрах 30% раствора кислоты в воде содержится
![]()
литров кислоты. В 9 литрах 80% раствора кислоты в воде содержится
![]()
литров кислоты. Поэтому в смеси этих растворов содержится
4,8 + 7,2 = 12
литров кислоты. Поскольку полученный в результате смешивания раствор имеет объем
16 + 9 = 25
литров, то концентрация кислоты в этом растворе равна
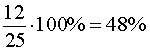
Ответ. 48% .
Задача 2. Имеется 27 килограммов смеси цемента с песком с 40% содержанием цемента. Сколько килограммов песка нужно добавить в эту смесь, чтобы процентное содержание цемента в ней стало 30% ?
Решение. Обозначим буквой x количество килограммов песка, которые нужно добавить в смесь. Поскольку в 27 килограммах смеси с 40% содержанием цемента содержится
![]()
килограммов цемента, а после добавления x килограммов песка масса смеси станет равной
27 + x
килограммов, то после добавления песка процентное содержание цемента в получившейся смеси будет составлять
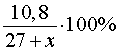
По условию задачи
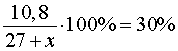
Следовательно,
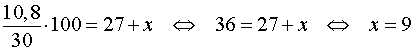
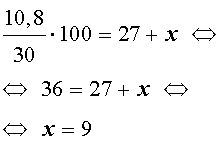
Ответ. 9 килограммов.
Задача 3. Смешав 8% и 13% растворы соли и добавив 200 миллилитров 5% раствора соли, получили 7% раствор соли. Если бы вместо 200 миллилитров 5% раствора соли добавили 300 миллилитров 17% раствора соли, то получили бы 15% раствор соли. Сколько миллилитров 8% и 13% растворов соли использовали для получения раствора?
Решение. Обозначив буквой x массу 8% раствора соли, а буквой y – массу 13% раствора соли, рассмотрим рисунки 1 и 2.
| x мл | |||
| |||
| + | y мл | ||
| |||
| + | 200 мл | ||
| |||
| = | (x + y + 200) мл | ||
|
Рис. 1
На рисунке 1 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 200 миллилитров 9% раствора соли. Объем этого раствора равен (x + y + 200) миллилитров.
| x мл | |||
| |||
| + | y мл | ||
| |||
| + | 300 мл | ||
| |||
| = | (x + y + 300) мл | ||
|
Рис.2
На рисунке 2 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 300 миллилитров 17% раствора соли. Объем этого раствора равен (x + y + 300) миллилитров.
Записывая баланс соли в растворе, структура которого изображена на рисунке 1, а также баланс соли в растворе, структура которого изображена на рисунке 2, получим систему из двух уравнений с двумя неизвестными x и y :
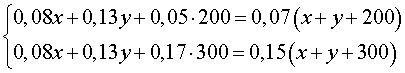
Раскрывая скобки и приводя подобные члены, получаем
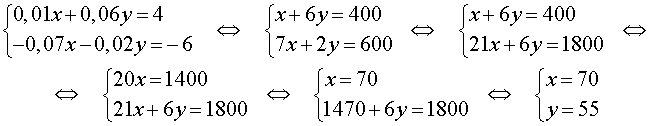
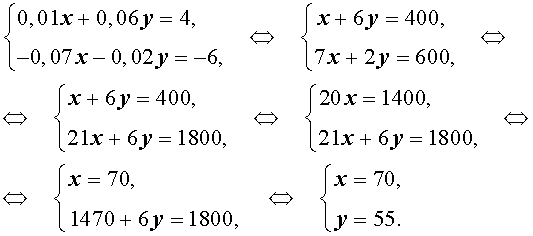
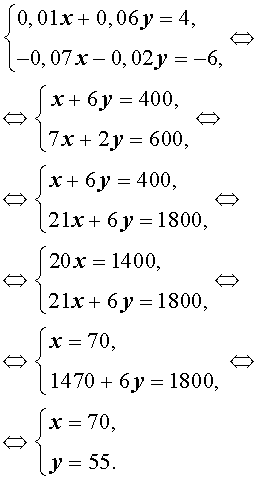
Ответ. Смешали 70 мл 8% раствора и 55 мл 13% раствора.
Задача 4. Имеются два сплава меди с цинком. Если сплавить 1 килограмм первого сплава с 2 килограммами второго сплава, то получится сплав с 50% содержанием меди. Если же сплавить 4 килограмма первого сплава с 1 килограммом второго сплава, то получится сплав с 36% содержанием меди. Найти процентное содержание меди в первом и во втором сплавах.
Решение. Обозначим x % и y % - процентные содержания меди в первом и во втором сплавах соответственно и рассмотрим рисунки 3 и 4.
| 1 кг | 2 кг | |||||||||
| Медь x % | Цинк | + | Медь y % | Цинк | ||||||
| ||||||||||
Рис. 3
На рисунке 3 изображена структура сплава, состоящего из 1 килограмма первого сплава и 2 килограммов второго сплава. Масса этого сплава – 3 килограмма.
| 4 кг | 1 кг | |||||||||
| Медь x % | Цинк | + | Медь y % | Цинк | ||||||
| ||||||||||
Рис.4
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Записывая баланс меди в сплаве, структура которого изображена на рисунке 3, а также баланс меди в сплаве, структура которого изображена на рисунке 4, получим систему из двух уравнений с двумя неизвестными x и y :
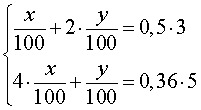
Далее получаем
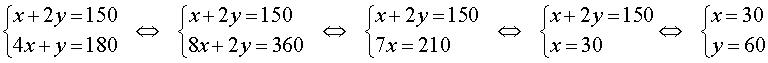
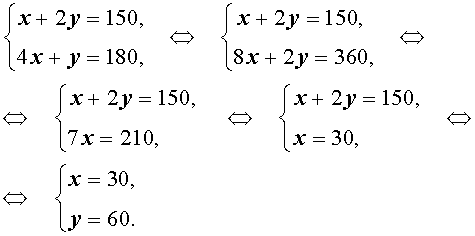
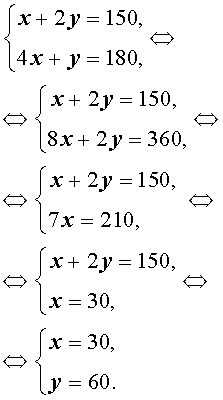
Ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .

Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть раздел нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ, представлены в разделе нашего справочника «Задачи на выполнение работ».
С примерами решения задач на движение можно ознакомиться в разделе нашего справочника «Задачи на движение».
С методами решения систем уравнений можно ознакомиться в разделах нашего справочника «Системы линейных уравнений», «Системы с нелинейными уравнениями» и в нашем учебном пособии «Системы уравнений».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
