Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
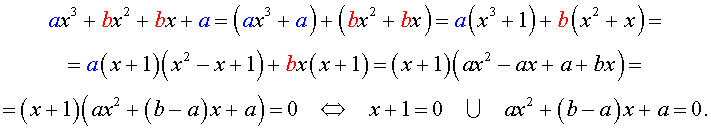
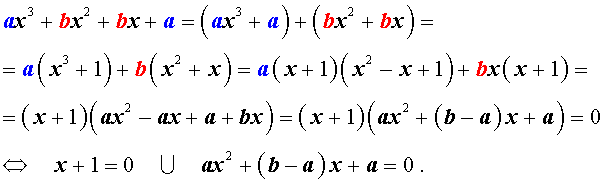
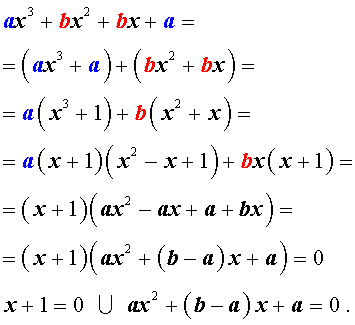
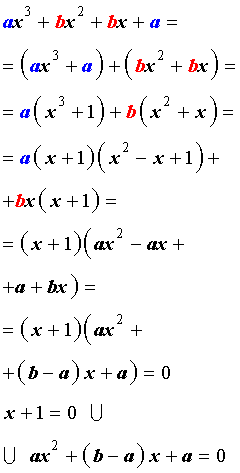
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
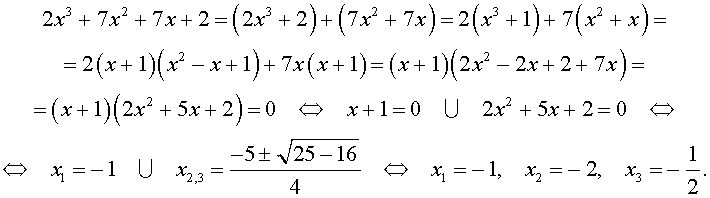
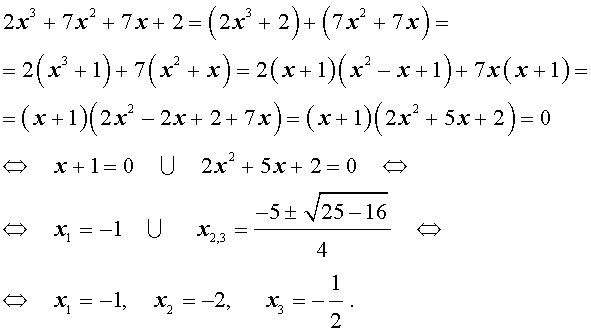
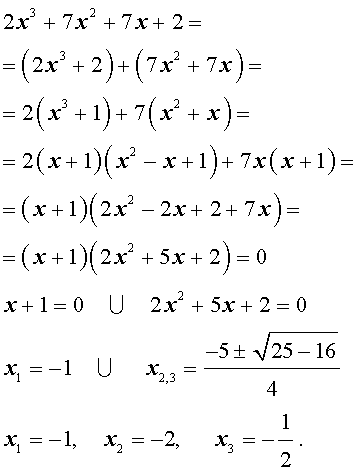
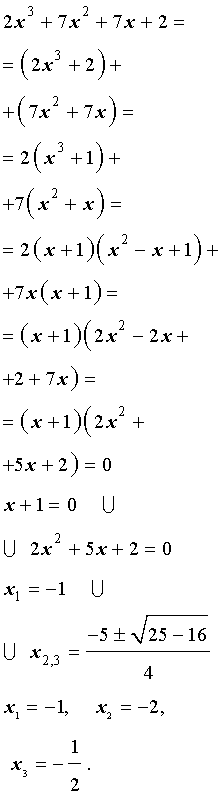
Ответ: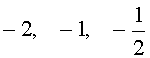 .
.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2 – – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
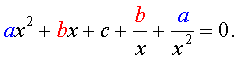 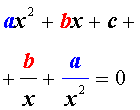 | (5) |
Преобразуем левую часть уравнения (5):
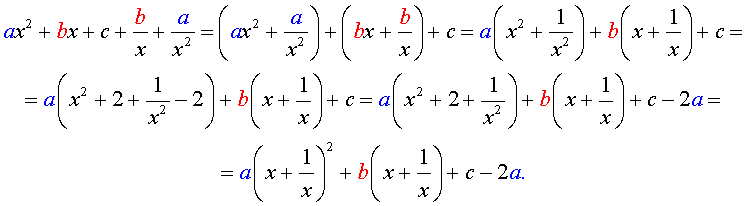
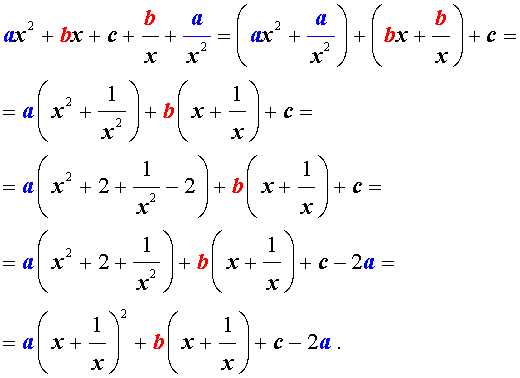
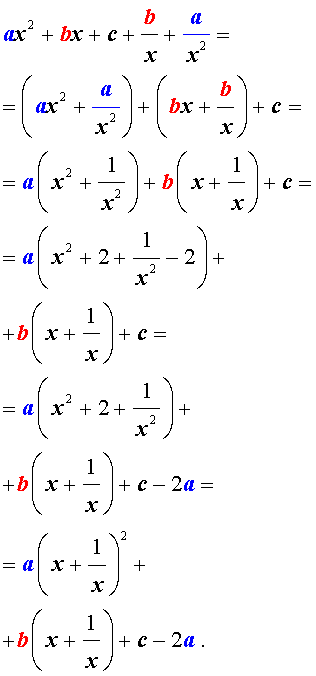
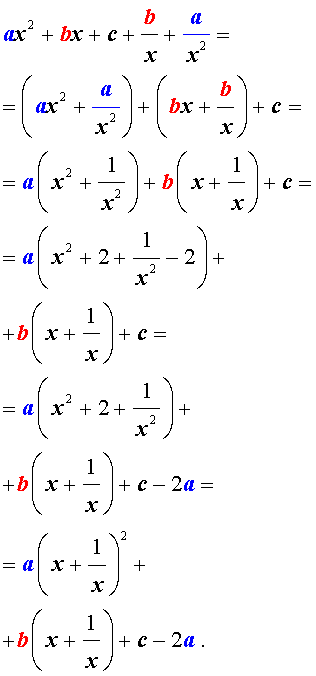
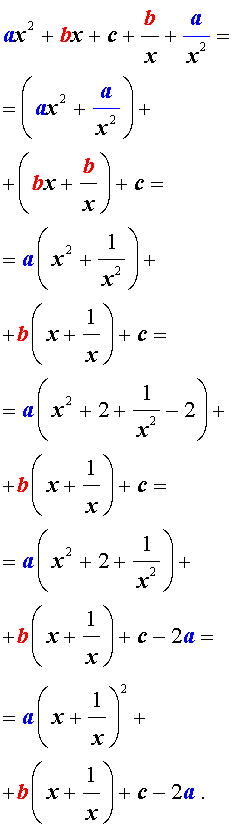
В результате этого преобразования уравнение (5) принимает вид
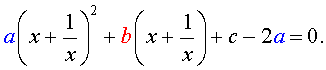 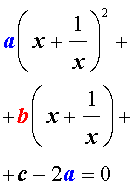 | (6) |
Если теперь обозначить
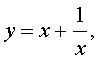 | (7) |
то уравнение (6) станет квадратным уравнением:
| ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
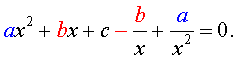 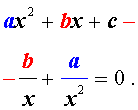 | (9) |
Преобразуем левую часть уравнения (9):
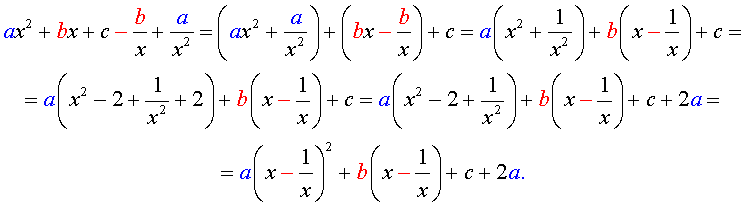
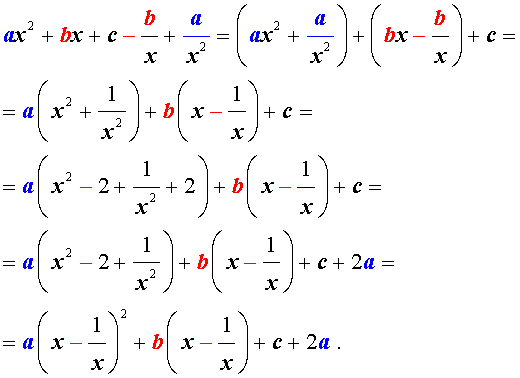
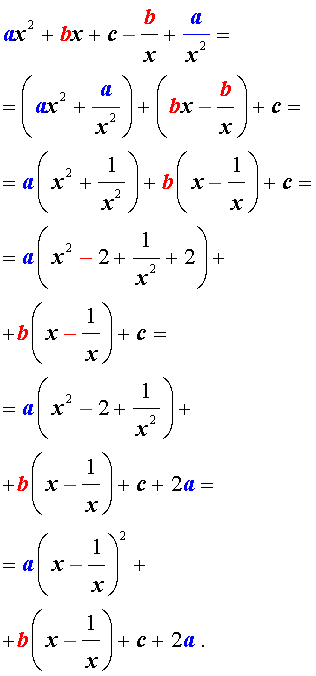
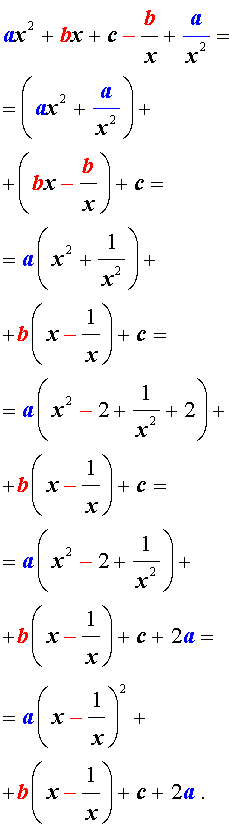
В результате этого преобразования уравнение (9) принимает вид
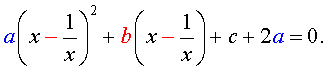 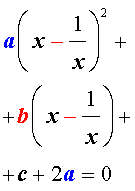 | (10) |
Если теперь обозначить
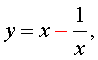 | (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0. | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
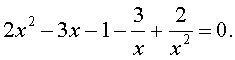 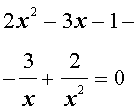 | (14) |
Преобразуем левую часть уравнения (14):
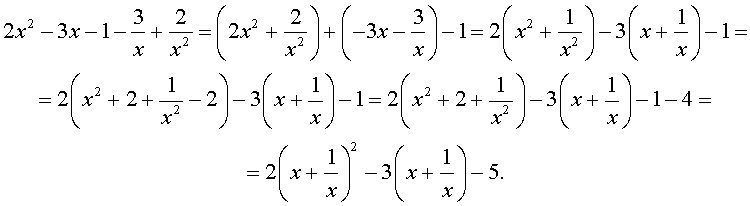
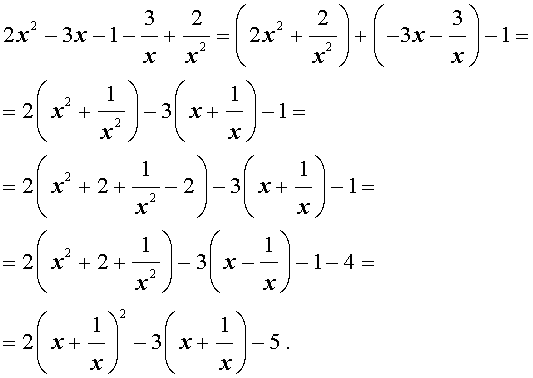
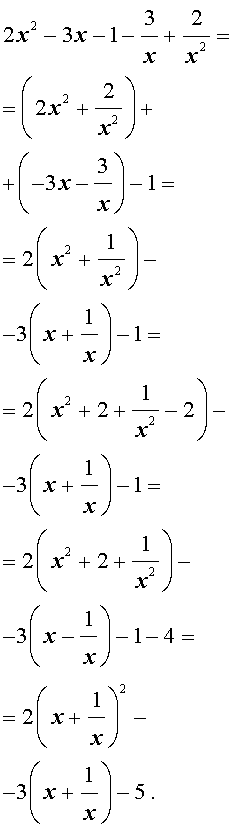
В результате этого преобразования уравнение (14) принимает вид
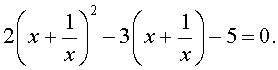 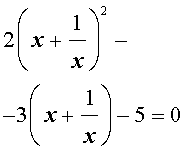 | (15) |
Если теперь обозначить
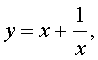 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y2 – 3y – 5 = 0. | (17) |
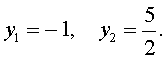 | (18) |
В первом случае из равенства (16) получаем уравнение:
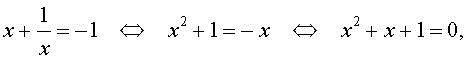
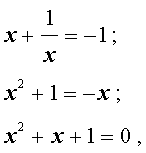
которое решений не имеет.
Во втором случае из равенства (16) получаем:
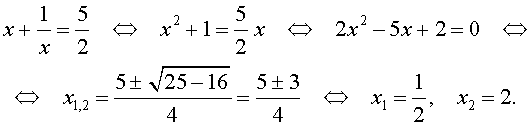
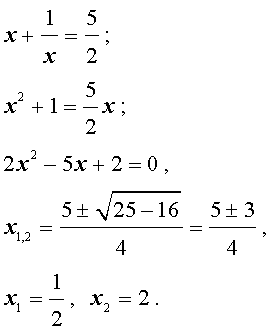
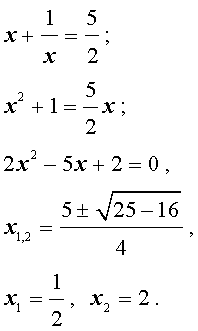
Ответ: 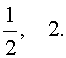
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
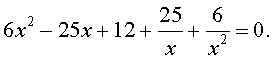 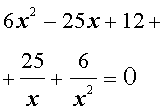 | (20) |
Преобразуем левую часть уравнения (20):
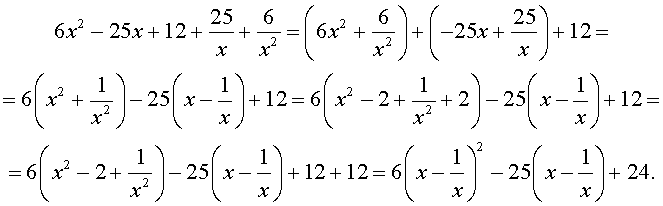
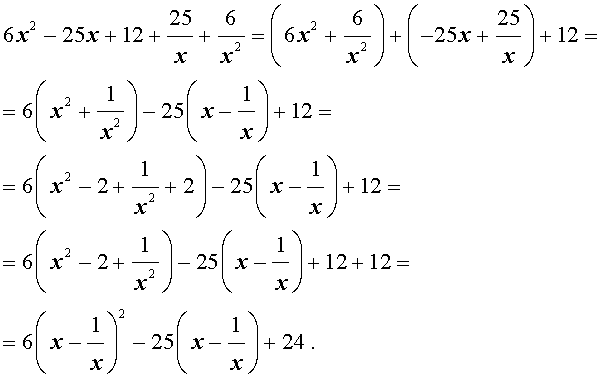
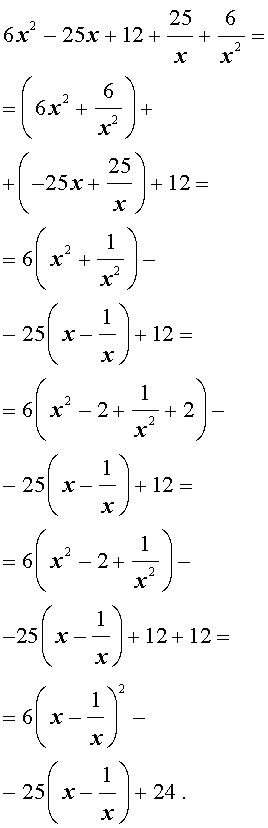
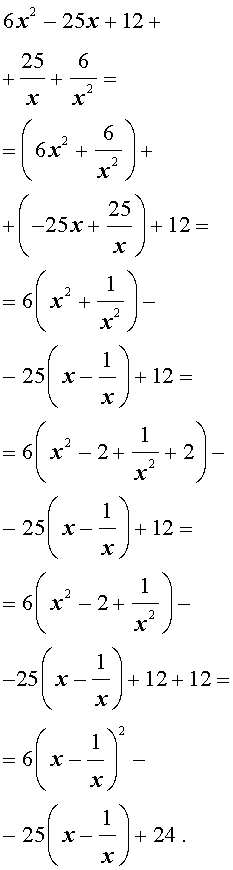
В результате этого преобразования уравнение (20) принимает вид
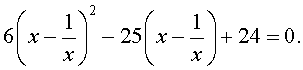 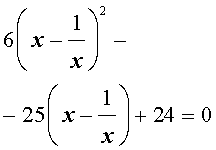 | (21) |
Если теперь обозначить
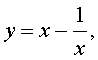 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y2 – 25y + 24 = 0. | (23) |
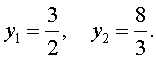 | (24) |
В первом случае из равенства (22) получаем:
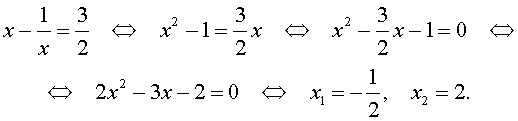
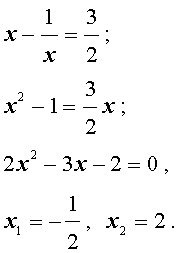
Во втором случае из равенства (22) получаем:
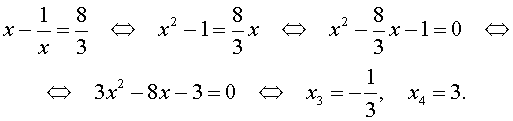
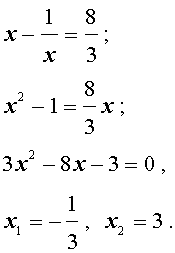
Ответ: 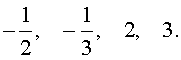
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
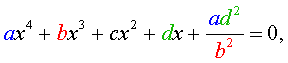 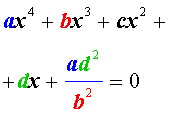 | (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
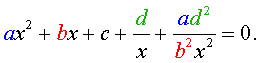 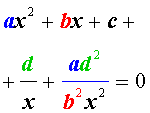 | (26) |
Преобразуем левую часть уравнения (26):
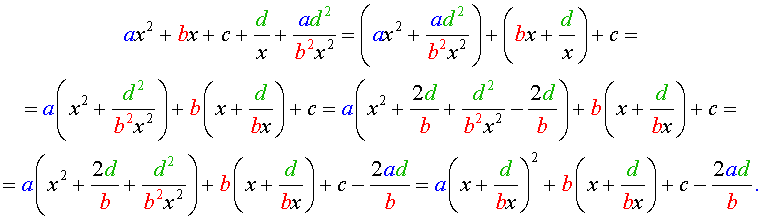
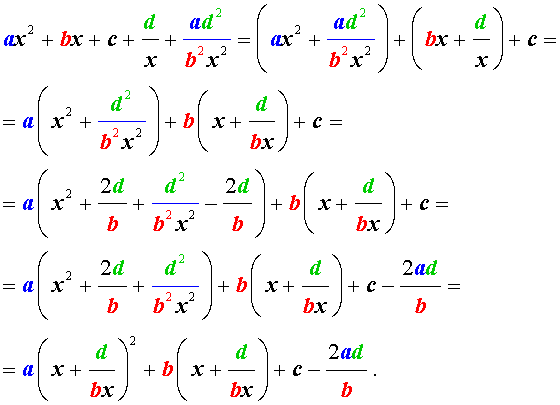
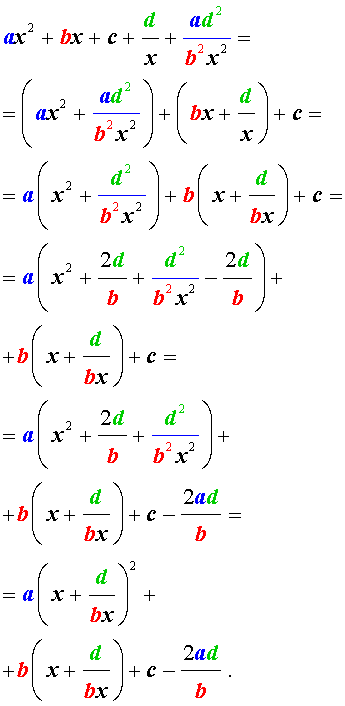
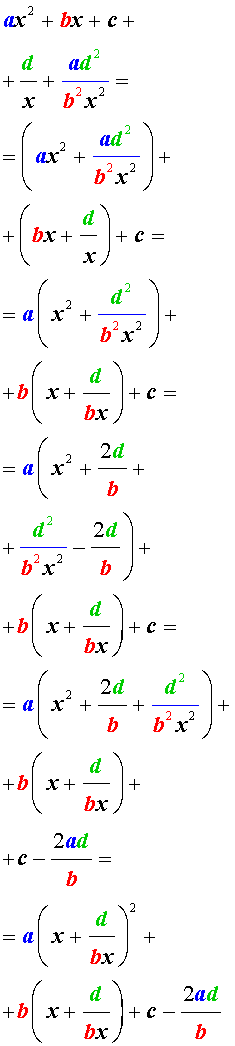
В результате этого преобразования уравнение (26) принимает вид
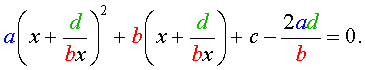 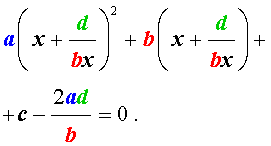 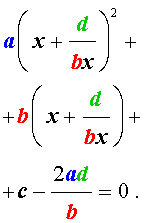 | (27) |
Если теперь обозначить
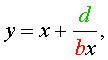 | (28) |
то уравнение (27) станет квадратным уравнением:
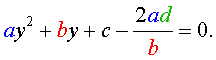 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
c = 35, d = – 30,
и найдем значение выражения
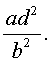
Поскольку
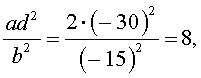
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
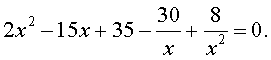 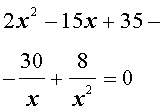 | (31) |
Преобразуем левую часть уравнения (31):
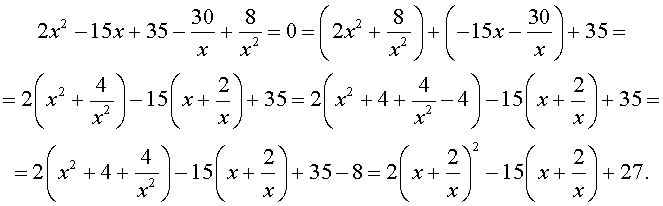
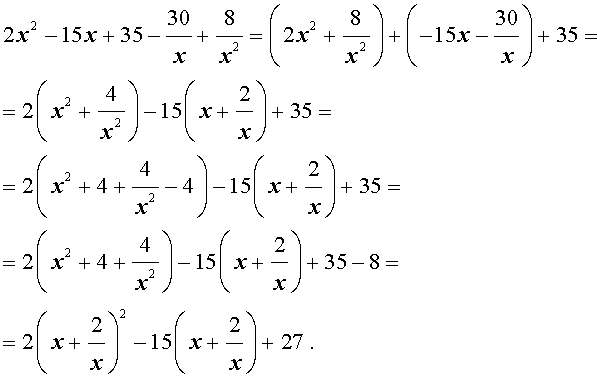
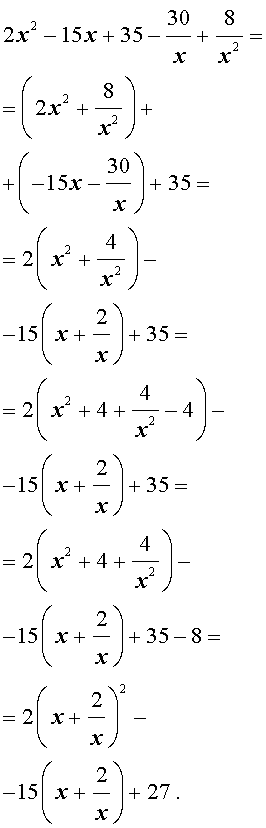
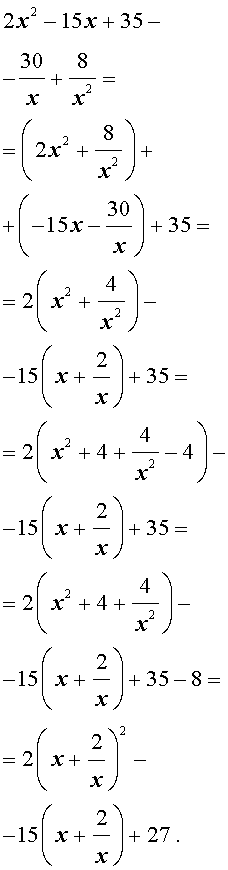
В результате этого преобразования уравнение (31) принимает вид
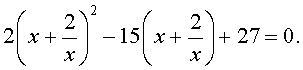 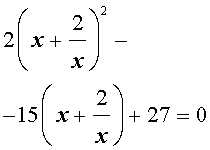 | (32) |
Если теперь обозначить
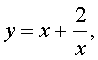 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y2 – 15y + 27 = 0. | (34) |
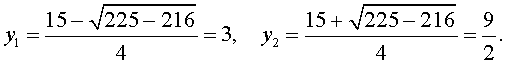
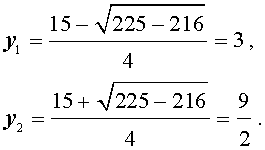
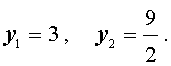
В первом случае из равенства (33) получаем:
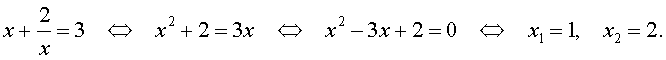
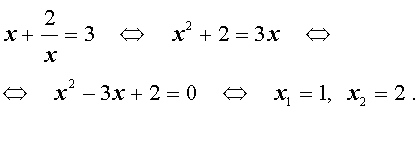
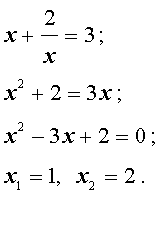
Во втором случае из равенства (33) получаем:
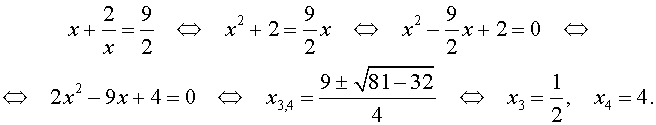
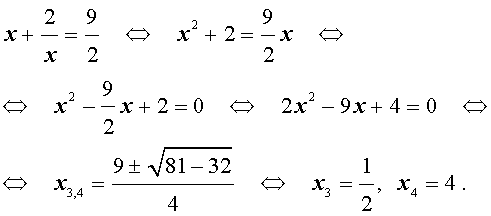
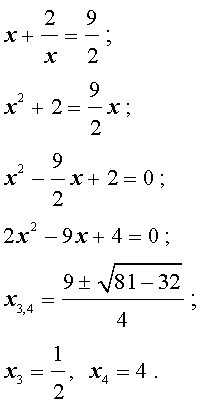
Ответ: 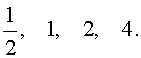

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |

