Справочник по математике

Алгебра

Последовательности чисел

Конечные числовые суммы. Метод математической индукции

Конечные числовые суммы

Метод математической индукции

Конечные числовые суммы

      Пусть   n   – произвольное натуральное число. Тогда справедливы следующие формулы, которые называют конечными числовыми суммами:

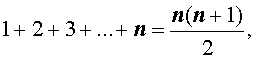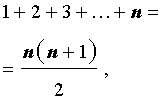	1 + 3 + 5 + … + (2n – 1) = = n2 ,
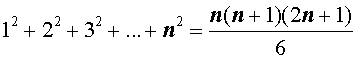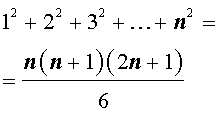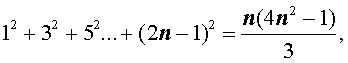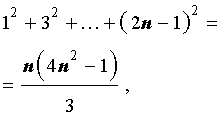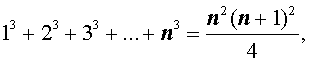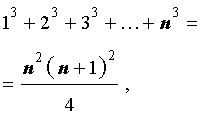	13 + 33 + 53 + … + (2n – 1)3 = = n2 (2n2 – 1) ,

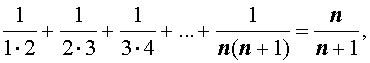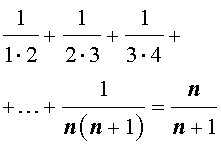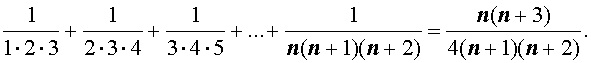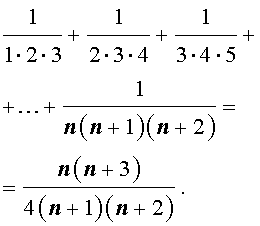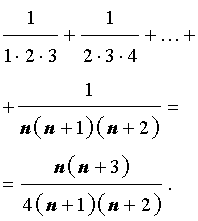      Сумма бесконечно убывающей геометрической прогрессии является простейшим примером бесконечной числовой суммы (числового ряда). Ряды изучают в ВУЗовских курсах математики.

      Доказательство формул для конечных числовых сумм можно получить с помощью различных методов.

      К изложению одного из мощнейших методов доказательства этих, а также подобных формул, – методу (принципу) математической индукции мы сейчас и переходим.

Метод математической индукции

      Предположим, что нам требуется доказать, что некоторая формула верна при любом натуральном значении   n .   Предположим также, что мы:

1. непосредственно проверили, что формула верна при   n = 1 ,
2. доказали, что из справедливости формулы для некоторого номера   n ,   вытекает её справедливость для номера   n + 1 .

      Тогда в силу метода (принципа) математической индукции можно утверждать, что формула верна для всех натуральных чисел   n .

      Для примера дадим доказательство одной из формул, приведенных в предыдущем разделе.

      Пример 1. Доказать, что при всех натуральных   n   верна формула

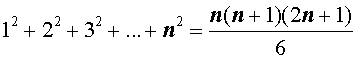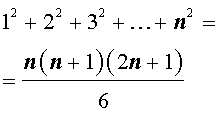(1)

      Решение. Для доказательства воспользуемся методом математической индукции:

1. В случае   n = 1   формула (1) имеет вид

   

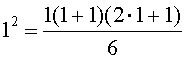
   и является верной.

2. Докажем, что из справедливости равенства (1), вытекает справедливость равенства

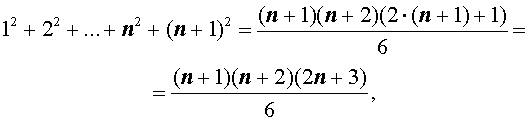
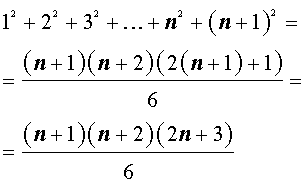
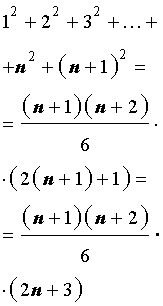
   (2)

   полученного из равенства (1) при помощи замены   n   на   n + 1 .

         Действительно,

   
   

   

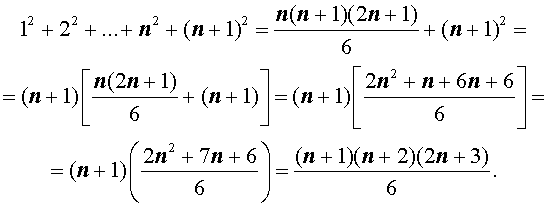
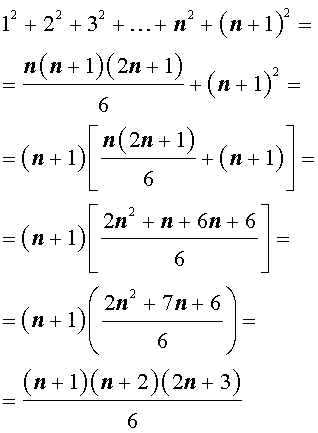
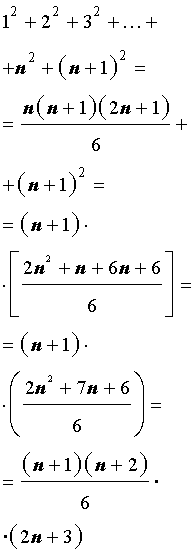
         Следовательно, формула (2) верна, откуда из принципа математической индукции заключаем, что формула (1) верна для всех натуральных значений   n .

      Пример 2. Доказать, что число   n⁵ – n   делится на   5   при всех натуральных значениях n .

      Решение. Для доказательства снова воспользуемся методом математической индукции:

1. В случае   n = 1   число   n⁵ – n   равно   0   и, конечно же, делится на   5 .

   Таким образом, при   n = 1   требуемое утверждение верно.

2. Теперь докажем, что из того, что число   n⁵ – n   делится на   5   вытекает, что число

   (n + 1)⁵ – (n + 1)

   также делится на   5 .

         Действительно, пусть

   n⁵ – n = 5k ,

   где   .

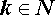         Тогда поскольку

   (n + 1)⁵ = n⁵ + 5n⁴ +
   + 10n³ + 10n² + 5n + 1

   (см. Таблицу 1 из раздела справочника «Формулы сокращенного умножения: степень суммы и степень разности»), то

   (n + 1)⁵ – (n + 1) =
   = (n⁵ – n)+
   + 5n⁴ +
   + 10n³ + 10n² + 5n =
   = 5k + 5n⁴ + 10n³ +
   + 10n² + 5n =
   = 5 (k + n⁴ +
   + 2n³ + 2n² + n) ,

   т.е. делится на   5 .

         В соответствии с принципом математической индукции все доказано.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.